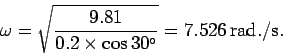Next: Non-uniform circular motion
Up: Circular motion
Previous: Centripetal acceleration
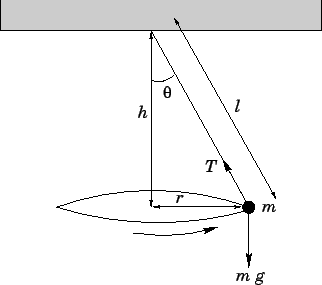
Suppose that an object, mass  , is attached to the end of a light inextensible
string whose other end is attached to a rigid beam. Suppose, further, that the
object is given an initial horizontal velocity such that it executes a
horizontal circular orbit of radius
, is attached to the end of a light inextensible
string whose other end is attached to a rigid beam. Suppose, further, that the
object is given an initial horizontal velocity such that it executes a
horizontal circular orbit of radius  with angular velocity
with angular velocity  . See
Fig. 60. Let
. See
Fig. 60. Let 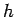 be the vertical distance between the beam and the plane of
the circular orbit, and let
be the vertical distance between the beam and the plane of
the circular orbit, and let  be the angle subtended by the string with
the downward vertical.
be the angle subtended by the string with
the downward vertical.
Figure 60:
A conical pendulum.
 |
The object is subject to two forces: the gravitational force  which acts vertically
downwards, and the tension force
which acts vertically
downwards, and the tension force 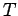 which acts upwards along the string. The tension
force can be resolved into a component
which acts upwards along the string. The tension
force can be resolved into a component 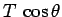 which acts vertically upwards, and
a component
which acts vertically upwards, and
a component 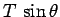 which acts towards the centre of the circle. Force balance
in the vertical direction yields
which acts towards the centre of the circle. Force balance
in the vertical direction yields
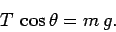 |
(262) |
In other words, the vertical component of the tension force balances the weight of the object.
Since the object is executing a circular orbit, radius  , with angular velocity
, with angular velocity  ,
it experiences a centripetal acceleration
,
it experiences a centripetal acceleration 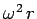 . Hence, it is subject to
a centripetal force
. Hence, it is subject to
a centripetal force
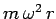 . This force is provided by the component of
the string tension which acts towards the centre of the circle. In other words,
. This force is provided by the component of
the string tension which acts towards the centre of the circle. In other words,
 |
(263) |
Taking the ratio of Eqs. (262) and (263), we obtain
 |
(264) |
However, by simple trigonometry,
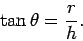 |
(265) |
Hence, we find
 |
(266) |
Note that if 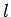 is the length of the string then
is the length of the string then
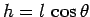 . It follows that
. It follows that
 |
(267) |
For instance, if the length of the string is
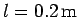 and the conical angle is
and the conical angle is
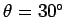 then the angular velocity of rotation is given by
then the angular velocity of rotation is given by
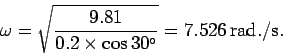 |
(268) |
This translates to a rotation frequency in cycles per second of
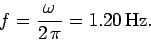 |
(269) |



Next: Non-uniform circular motion
Up: Circular motion
Previous: Centripetal acceleration
Richard Fitzpatrick
2006-02-02

![]() which acts vertically
downwards, and the tension force
which acts vertically
downwards, and the tension force ![]() which acts upwards along the string. The tension
force can be resolved into a component
which acts upwards along the string. The tension
force can be resolved into a component ![]() which acts vertically upwards, and
a component
which acts vertically upwards, and
a component ![]() which acts towards the centre of the circle. Force balance
in the vertical direction yields
which acts towards the centre of the circle. Force balance
in the vertical direction yields
![]() , with angular velocity
, with angular velocity ![]() ,
it experiences a centripetal acceleration
,
it experiences a centripetal acceleration ![]() . Hence, it is subject to
a centripetal force
. Hence, it is subject to
a centripetal force
![]() . This force is provided by the component of
the string tension which acts towards the centre of the circle. In other words,
. This force is provided by the component of
the string tension which acts towards the centre of the circle. In other words,

![]() and the conical angle is
and the conical angle is
![]() then the angular velocity of rotation is given by
then the angular velocity of rotation is given by