


Next: Centripetal acceleration
Up: Circular motion
Previous: Introduction
Suppose that an object executes a circular orbit of radius
 with uniform tangential speed
with uniform tangential speed  . The instantaneous
position of the object is most conveniently specified in terms of an
angle
. The instantaneous
position of the object is most conveniently specified in terms of an
angle  . See Fig. 57. For instance, we could decide that
. See Fig. 57. For instance, we could decide that
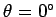 corresponds
to the object's location at
corresponds
to the object's location at  , in which case we would write
, in which case we would write
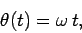 |
(245) |
where  is termed the angular velocity of the object. For a uniformly
rotating object, the angular velocity is simply the angle through which the object
turns in one second.
is termed the angular velocity of the object. For a uniformly
rotating object, the angular velocity is simply the angle through which the object
turns in one second.
Figure 57:
Circular motion.
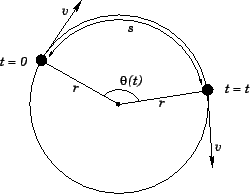 |
Consider the motion of the object in the time interval between
 and
and 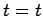 . In this interval, the object rotates through an angle
. In this interval, the object rotates through an angle
 , and traces out a circular arc of length
, and traces out a circular arc of length  . See Fig. 57.
It is fairly obvious that the arc length
. See Fig. 57.
It is fairly obvious that the arc length  is directly proportional to the angle
is directly proportional to the angle
 : but, what is the constant of proportionality? Well, an angle of
: but, what is the constant of proportionality? Well, an angle of
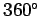 corresponds to an arc length of
corresponds to an arc length of 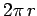 . Hence, an angle
. Hence, an angle  must correspond to an arc length of
must correspond to an arc length of
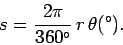 |
(246) |
At this stage, it is convenient to define a new angular unit known as a radian (symbol rad.). An angle
measured in radians is related to an angle measured in degrees via the
following simple formula:
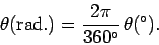 |
(247) |
Thus, 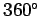 corresponds to
corresponds to 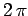 radians,
radians, 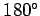 corresponds to
corresponds to 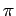 radians,
radians,
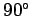 corresponds to
corresponds to 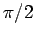 radians, and
radians, and 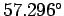 corresponds
to 1 radian. When
corresponds
to 1 radian. When  is measured in radians, Eq. (246) simplifies
greatly to give
is measured in radians, Eq. (246) simplifies
greatly to give
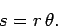 |
(248) |
Henceforth, in this course, all angles are measured in radians by default.
Consider the motion of the object in the short interval between times  and
and 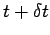 .
In this interval, the object turns through a small angle
.
In this interval, the object turns through a small angle 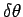 and
traces out a short arc of length
and
traces out a short arc of length 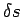 , where
, where
 |
(249) |
Now
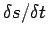 (i.e., distance moved per unit time)
is simply the tangential velocity
(i.e., distance moved per unit time)
is simply the tangential velocity  , whereas
, whereas
 (i.e., angle turned through per unit time) is simply the angular velocity
(i.e., angle turned through per unit time) is simply the angular velocity
 . Thus, dividing Eq. (249) by
. Thus, dividing Eq. (249) by  , we obtain
, we obtain
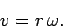 |
(250) |
Note, however, that this formula is only valid if the angular velocity
 is measured in radians per second. From now on, in this
course, all angular velocities are measured in radians per second by default.
is measured in radians per second. From now on, in this
course, all angular velocities are measured in radians per second by default.
An object that rotates with uniform angular velocity  turns through
turns through
 radians in 1 second. Hence, the object turns through
radians in 1 second. Hence, the object turns through 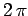 radians
(i.e., it executes a complete circle) in
radians
(i.e., it executes a complete circle) in
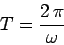 |
(251) |
seconds. Here, 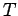 is the repetition period of the circular motion. If the object
executes a complete cycle (i.e., turns through
is the repetition period of the circular motion. If the object
executes a complete cycle (i.e., turns through 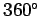 ) in
) in 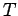 seconds,
then the number of cycles executed per second is
seconds,
then the number of cycles executed per second is
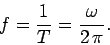 |
(252) |
Here, the repetition frequency, 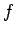 , of the motion is measured in
cycles per second--otherwise known as hertz (symbol Hz).
, of the motion is measured in
cycles per second--otherwise known as hertz (symbol Hz).
As an example, suppose that an object executes uniform circular motion, radius
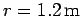 , at a frequency of
, at a frequency of
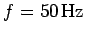 (i.e., the object executes a complete
rotation 50 times a second). The repetition period of this motion is simply
(i.e., the object executes a complete
rotation 50 times a second). The repetition period of this motion is simply
 |
(253) |
Furthermore, the angular frequency of the motion is given by
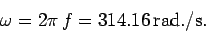 |
(254) |
Finally, the tangential velocity of the object is
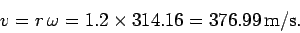 |
(255) |



Next: Centripetal acceleration
Up: Circular motion
Previous: Introduction
Richard Fitzpatrick
2006-02-02
![]() and
and ![]() . In this interval, the object rotates through an angle
. In this interval, the object rotates through an angle
![]() , and traces out a circular arc of length
, and traces out a circular arc of length ![]() . See Fig. 57.
It is fairly obvious that the arc length
. See Fig. 57.
It is fairly obvious that the arc length ![]() is directly proportional to the angle
is directly proportional to the angle
![]() : but, what is the constant of proportionality? Well, an angle of
: but, what is the constant of proportionality? Well, an angle of
![]() corresponds to an arc length of
corresponds to an arc length of ![]() . Hence, an angle
. Hence, an angle ![]() must correspond to an arc length of
must correspond to an arc length of
![]() and
and ![]() .
In this interval, the object turns through a small angle
.
In this interval, the object turns through a small angle ![]() and
traces out a short arc of length
and
traces out a short arc of length ![]() , where
, where
![]() turns through
turns through
![]() radians in 1 second. Hence, the object turns through
radians in 1 second. Hence, the object turns through ![]() radians
(i.e., it executes a complete circle) in
radians
(i.e., it executes a complete circle) in
![]() , at a frequency of
, at a frequency of
![]() (i.e., the object executes a complete
rotation 50 times a second). The repetition period of this motion is simply
(i.e., the object executes a complete
rotation 50 times a second). The repetition period of this motion is simply