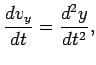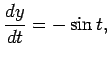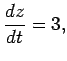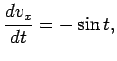Next: Motion with constant velocity
Up: Motion in 3 dimensions
Previous: Diagonals of a parallelogram
Consider a body moving in 3 dimensions. Suppose that we know the Cartesian
coordinates,  ,
,  , and
, and  , of this body as time,
, of this body as time,  , progresses.
Let us consider how we can use this information to determine the body's instantaneous
velocity and acceleration as functions of time.
, progresses.
Let us consider how we can use this information to determine the body's instantaneous
velocity and acceleration as functions of time.
The vector displacement of the body is given by
![\begin{displaymath}
{\bf r}(t) = [x(t), y(t), z(t)].
\end{displaymath}](img266.png) |
(43) |
By analogy with the 1-dimensional equation (13), the body's
vector velocity
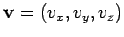 is simply the derivative of
is simply the derivative of  with respect to
with respect to
 . In other words,
. In other words,
 |
(44) |
When written in component form, the above definition yields
Thus, the  -component of velocity is simply the time derivative of the
-component of velocity is simply the time derivative of the  -coordinate,
and so on.
-coordinate,
and so on.
By analogy with the 1-dimensional equation (16), the body's
vector acceleration
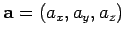 is simply the derivative of
is simply the derivative of 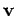 with respect to
with respect to
 . In other words,
. In other words,
 |
(48) |
When written in component form, the above definition yields
Thus, the  -component of acceleration is simply the time derivative
of the
-component of acceleration is simply the time derivative
of the  -component of velocity, and so on.
-component of velocity, and so on.
As an example, suppose that the coordinates of the body are given by
The corresponding components of the body's velocity are then simply
whilst the components of the body's acceleration are given by



Next: Motion with constant velocity
Up: Motion in 3 dimensions
Previous: Diagonals of a parallelogram
Richard Fitzpatrick
2006-02-02
![]() is simply the derivative of
is simply the derivative of ![]() with respect to
with respect to
![]() . In other words,
. In other words,