


Next: Vector velocity and vector
Up: Motion in 3 dimensions
Previous: Scalar multiplication
The use of vectors is very well illustrated by the following rather famous proof
that the diagonals of a parallelogram mutually bisect one another.
Figure 13:
A parallelogram
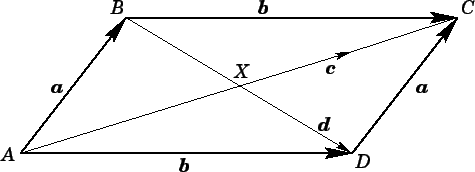 |
Suppose that the quadrilateral ABCD in Fig. 13 is a parallelogram. It follows that
the opposite sides of ABCD can be represented by the
same vectors,  and
and 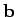 : this merely indicates that these sides are of
equal length and are parallel (i.e., they point in the same direction). Note that
Fig. 13 illustrates an important point regarding vectors. Although vectors possess
both a magnitude (length) and a direction, they possess no intrinsic position information.
Thus, since sides
: this merely indicates that these sides are of
equal length and are parallel (i.e., they point in the same direction). Note that
Fig. 13 illustrates an important point regarding vectors. Although vectors possess
both a magnitude (length) and a direction, they possess no intrinsic position information.
Thus, since sides 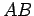 and
and 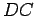 are parallel and of equal length, they can be represented
by the same vector
are parallel and of equal length, they can be represented
by the same vector  , despite the fact that they are in different places on the
diagram.
, despite the fact that they are in different places on the
diagram.
The diagonal 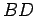 in Fig. 13 can be represented vectorially as
in Fig. 13 can be represented vectorially as
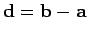 .
Likewise, the diagonal
.
Likewise, the diagonal 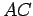 can be written
can be written
 .
The displacement
.
The displacement 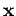 (say) of the centroid
(say) of the centroid 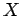 from point
from point  can be written in one
of two different ways:
can be written in one
of two different ways:
Equation (38) is interpreted as follows: in order to get from point  to point
to point 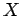 ,
first move to point
,
first move to point  (along vector
(along vector  ), then move along diagonal
), then move along diagonal 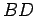 (along
vector
(along
vector 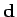 ) for an unknown fraction
) for an unknown fraction 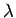 of its length.
Equation (39) is interpreted as follows: in order to get from point
of its length.
Equation (39) is interpreted as follows: in order to get from point  to point
to point
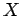 , first move to point
, first move to point  (along vector
(along vector 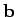 ), then move to point
), then move to point  (along vector
(along vector  ), finally move along diagonal
), finally move along diagonal  (along vector
(along vector
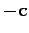 ) for an unknown fraction
) for an unknown fraction  of its length. Since
of its length. Since 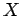 represents the
same point in Eqs. (38) and (39), we can equate these two
expressions to give
represents the
same point in Eqs. (38) and (39), we can equate these two
expressions to give
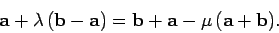 |
(40) |
Now vectors  and
and 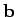 point in different directions, so the only way
in which the above expression can be satisfied, in general, is if the coefficients of
point in different directions, so the only way
in which the above expression can be satisfied, in general, is if the coefficients of
 and
and 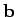 match on either side of the equality sign. Thus,
equating coefficients of
match on either side of the equality sign. Thus,
equating coefficients of  and
and 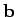 , we obtain
, we obtain
It follows that
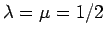 . In other words, the centroid
. In other words, the centroid 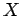 is located at
the halfway points of diagonals
is located at
the halfway points of diagonals 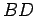 and
and 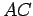 : i.e., the diagonals
mutually bisect one another.
: i.e., the diagonals
mutually bisect one another.



Next: Vector velocity and vector
Up: Motion in 3 dimensions
Previous: Scalar multiplication
Richard Fitzpatrick
2006-02-02

![]() and
and ![]() : this merely indicates that these sides are of
equal length and are parallel (i.e., they point in the same direction). Note that
Fig. 13 illustrates an important point regarding vectors. Although vectors possess
both a magnitude (length) and a direction, they possess no intrinsic position information.
Thus, since sides
: this merely indicates that these sides are of
equal length and are parallel (i.e., they point in the same direction). Note that
Fig. 13 illustrates an important point regarding vectors. Although vectors possess
both a magnitude (length) and a direction, they possess no intrinsic position information.
Thus, since sides ![]() and
and ![]() are parallel and of equal length, they can be represented
by the same vector
are parallel and of equal length, they can be represented
by the same vector ![]() , despite the fact that they are in different places on the
diagram.
, despite the fact that they are in different places on the
diagram.
![]() in Fig. 13 can be represented vectorially as
in Fig. 13 can be represented vectorially as
![]() .
Likewise, the diagonal
.
Likewise, the diagonal ![]() can be written
can be written
![]() .
The displacement
.
The displacement ![]() (say) of the centroid
(say) of the centroid ![]() from point
from point ![]() can be written in one
of two different ways:
can be written in one
of two different ways: