


Next: Jointed rods
Up: Statics
Previous: Rods and cables
Suppose that a ladder of length 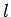 and negligible mass is leaning against a
vertical wall, making an angle
and negligible mass is leaning against a
vertical wall, making an angle  with the horizontal.
A workman of mass
with the horizontal.
A workman of mass  climbs a distance
climbs a distance  along the ladder,
measured from
the bottom. See Fig. 93.
Suppose that the wall is completely frictionless, but that the ground
possesses a coefficient of static friction
along the ladder,
measured from
the bottom. See Fig. 93.
Suppose that the wall is completely frictionless, but that the ground
possesses a coefficient of static friction  . How far up the ladder can the
workman climb before it slips along the ground? Is it possible for the workman to climb to
the top of the ladder without any slippage occurring?
. How far up the ladder can the
workman climb before it slips along the ground? Is it possible for the workman to climb to
the top of the ladder without any slippage occurring?
Figure 93:
A ladder leaning against a vertical wall.
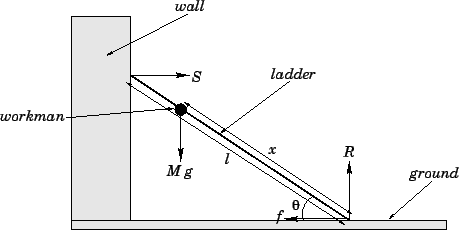 |
There are four forces acting on the ladder: the weight, 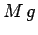 , of the workman; the
reaction,
, of the workman; the
reaction, 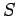 , at the wall; the reaction,
, at the wall; the reaction,  , at the ground; and the frictional force,
, at the ground; and the frictional force,
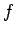 , due to the ground. The weight acts at the position of the workman, and is directed
vertically downwards. The reaction,
, due to the ground. The weight acts at the position of the workman, and is directed
vertically downwards. The reaction, 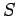 , acts at the top of the ladder, and is directed
horizontally (i.e., normal to the surface of the wall). The reaction,
, acts at the top of the ladder, and is directed
horizontally (i.e., normal to the surface of the wall). The reaction,  , acts at
the bottom of the ladder, and is directed vertically upwards (i.e., normal to the ground).
Finally, the frictional force,
, acts at
the bottom of the ladder, and is directed vertically upwards (i.e., normal to the ground).
Finally, the frictional force, 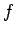 , also acts at the bottom of the ladder, and is directed
horizontally.
, also acts at the bottom of the ladder, and is directed
horizontally.
Resolving horizontally, and setting the net horizontal force acting on the ladder to
zero, we obtain
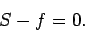 |
(483) |
Resolving vertically, and setting the net vertically force acting on the ladder to
zero, we obtain
 |
(484) |
Evaluating the torque acting about the point where the ladder touches the ground, we
note that only the forces 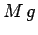 and
and 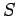 contribute. The lever arm associated with the
force
contribute. The lever arm associated with the
force 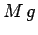 is
is 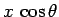 . The lever arm associated with the force
. The lever arm associated with the force 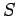 is
is 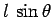 .
Furthermore, the torques associated with these two forces act in opposite directions.
Hence, setting the net torque about the bottom of the ladder to zero, we obtain
.
Furthermore, the torques associated with these two forces act in opposite directions.
Hence, setting the net torque about the bottom of the ladder to zero, we obtain
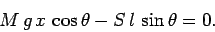 |
(485) |
The above three equations can be solved to give
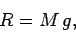 |
(486) |
and
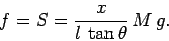 |
(487) |
Now, the condition for the ladder not to slip with respect to the ground is
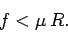 |
(488) |
This condition reduces to
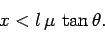 |
(489) |
Thus, the furthest distance that the workman can climb along the ladder before it
slips is
 |
(490) |
Note that if
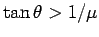 then the workman can climb all the way along the
ladder without any slippage occurring. This result suggests that ladders leaning against
walls are less likely to slip when they
are almost vertical (i.e., when
then the workman can climb all the way along the
ladder without any slippage occurring. This result suggests that ladders leaning against
walls are less likely to slip when they
are almost vertical (i.e., when
 ).
).



Next: Jointed rods
Up: Statics
Previous: Rods and cables
Richard Fitzpatrick
2006-02-02

![]() , of the workman; the
reaction,
, of the workman; the
reaction, ![]() , at the wall; the reaction,
, at the wall; the reaction, ![]() , at the ground; and the frictional force,
, at the ground; and the frictional force,
![]() , due to the ground. The weight acts at the position of the workman, and is directed
vertically downwards. The reaction,
, due to the ground. The weight acts at the position of the workman, and is directed
vertically downwards. The reaction, ![]() , acts at the top of the ladder, and is directed
horizontally (i.e., normal to the surface of the wall). The reaction,
, acts at the top of the ladder, and is directed
horizontally (i.e., normal to the surface of the wall). The reaction, ![]() , acts at
the bottom of the ladder, and is directed vertically upwards (i.e., normal to the ground).
Finally, the frictional force,
, acts at
the bottom of the ladder, and is directed vertically upwards (i.e., normal to the ground).
Finally, the frictional force, ![]() , also acts at the bottom of the ladder, and is directed
horizontally.
, also acts at the bottom of the ladder, and is directed
horizontally.