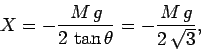Next: Worked example 10.1: Equilibrium
Up: Statics
Previous: Ladders and walls
Suppose that three identical uniform rods of mass  and length
and length 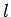 are joined together to form
an equilateral triangle, and are then suspended from a cable, as shown in
Fig. 94. What is the tension in the cable, and what
are the reactions at the joints?
are joined together to form
an equilateral triangle, and are then suspended from a cable, as shown in
Fig. 94. What is the tension in the cable, and what
are the reactions at the joints?
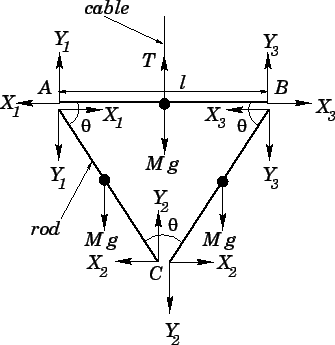
Figure 94:
Three identical jointed rods.
 |
Let 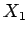 ,
,  , and
, and 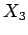 be the horizontal reactions at the three joints, and
let
be the horizontal reactions at the three joints, and
let  ,
, 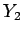 , and
, and  be the corresponding vertical reactions, as shown in Fig. 94.
In drawing this diagram, we have made use of the fact that the rods exert equal and
opposite reactions on one another, in accordance with Newton's third law. Let
be the corresponding vertical reactions, as shown in Fig. 94.
In drawing this diagram, we have made use of the fact that the rods exert equal and
opposite reactions on one another, in accordance with Newton's third law. Let 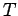 be the tension in the cable.
be the tension in the cable.
Setting the horizontal and vertical forces acting on rod 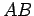 to zero, we obtain
to zero, we obtain
respectively.
Setting the horizontal and vertical forces acting on rod 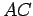 to zero, we obtain
to zero, we obtain
respectively.
Finally, setting the horizontal and vertical forces acting on rod  to zero, we obtain
to zero, we obtain
respectively.
Incidentally, it is clear, from symmetry, that 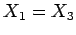 and
and 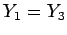 . Thus, the above equations can
be solved to give
. Thus, the above equations can
be solved to give
There now remains only one unknown, 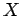 .
.
Now, it is clear, from symmetry, that there is zero net torque acting on rod 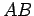 . Let us evaluate
the torque acting on rod
. Let us evaluate
the torque acting on rod 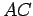 about point
about point  . (By symmetry, this
is the same as the torque acting on rod
. (By symmetry, this
is the same as the torque acting on rod  about point
about point  ). The two forces which contribute to
this torque are the weight,
). The two forces which contribute to
this torque are the weight, 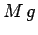 , and the reaction
, and the reaction 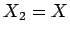 . (Recall that the reaction
. (Recall that the reaction 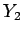 is zero). The lever arms associated with these two torques (which act in the same direction)
are
is zero). The lever arms associated with these two torques (which act in the same direction)
are
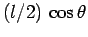 and
and 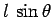 , respectively. Thus, setting the net torque
to zero, we obtain
, respectively. Thus, setting the net torque
to zero, we obtain
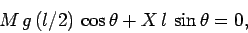 |
(501) |
which yields
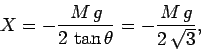 |
(502) |
since
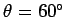 , and
, and
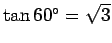 . We have now fully determined the
tension in the cable, and all the reactions
at the joints.
. We have now fully determined the
tension in the cable, and all the reactions
at the joints.



Next: Worked example 10.1: Equilibrium
Up: Statics
Previous: Ladders and walls
Richard Fitzpatrick
2006-02-02

![]() ,
, ![]() , and
, and ![]() be the horizontal reactions at the three joints, and
let
be the horizontal reactions at the three joints, and
let ![]() ,
, ![]() , and
, and ![]() be the corresponding vertical reactions, as shown in Fig. 94.
In drawing this diagram, we have made use of the fact that the rods exert equal and
opposite reactions on one another, in accordance with Newton's third law. Let
be the corresponding vertical reactions, as shown in Fig. 94.
In drawing this diagram, we have made use of the fact that the rods exert equal and
opposite reactions on one another, in accordance with Newton's third law. Let ![]() be the tension in the cable.
be the tension in the cable.
![]() to zero, we obtain
to zero, we obtain
![]() . Let us evaluate
the torque acting on rod
. Let us evaluate
the torque acting on rod ![]() about point
about point ![]() . (By symmetry, this
is the same as the torque acting on rod
. (By symmetry, this
is the same as the torque acting on rod ![]() about point
about point ![]() ). The two forces which contribute to
this torque are the weight,
). The two forces which contribute to
this torque are the weight, ![]() , and the reaction
, and the reaction ![]() . (Recall that the reaction
. (Recall that the reaction ![]() is zero). The lever arms associated with these two torques (which act in the same direction)
are
is zero). The lever arms associated with these two torques (which act in the same direction)
are
![]() and
and ![]() , respectively. Thus, setting the net torque
to zero, we obtain
, respectively. Thus, setting the net torque
to zero, we obtain