Ptolemy's aim in the Almagest is to construct a kinematic model of the solar system, as seen from the earth. In other words, the Almagest outlines a relatively simple geometric model which describes the apparent motions of the sun, moon, and planets, relative to the earth, but does not attempt to explain why these motions occur (in this respect, the models of Copernicus and Kepler are similar). As such, the fact that the model described in the Almagest is geocentric in nature is a non-issue, since the earth is stationary in its own frame of reference. This is not to say that the heliocentric hypothesis is without advantages. As we shall see, the assumption of heliocentricity allowed Copernicus to determine, for the first time, the ratios of the mean radii of the various planets in the solar system.
We now know, from the work of Kepler, that planetary orbits are actually ellipses
which are confocal with the sun. Such orbits possess two main properties.
First, they are eccentric: i.e., the sun is displaced from the
geometric center of the orbit. Second, they are elliptical: i.e.,
the orbit is elongated along a particular axis. Now, Keplerian orbits are characterized by a quantity, ![]() , called the eccentricity, which
measures their deviation from circularity. It is easily demonstrated
that the eccentricity of a Keplerian
orbit scales as
, called the eccentricity, which
measures their deviation from circularity. It is easily demonstrated
that the eccentricity of a Keplerian
orbit scales as ![]() , whereas the corresponding degree of elongation
scales as
, whereas the corresponding degree of elongation
scales as ![]() . Since the orbits of the visible planets in the solar system all possess relatively small values of
. Since the orbits of the visible planets in the solar system all possess relatively small values of ![]() (i.e.,
(i.e., ![]() ), it follows that, to an excellent approximation, these orbits can be represented as eccentric circles: i.e.,
circles which are not quite concentric with the sun. In other words,
we can neglect the ellipticities of planetary orbits compared to
their eccentricities.
This is exactly
what Ptolemy does in the Almagest.
It follows that Ptolemy's
assumption that heavenly bodies move in circles is actually
one of the main strengths of his model, rather than
being the main weakness, as is commonly
supposed.
), it follows that, to an excellent approximation, these orbits can be represented as eccentric circles: i.e.,
circles which are not quite concentric with the sun. In other words,
we can neglect the ellipticities of planetary orbits compared to
their eccentricities.
This is exactly
what Ptolemy does in the Almagest.
It follows that Ptolemy's
assumption that heavenly bodies move in circles is actually
one of the main strengths of his model, rather than
being the main weakness, as is commonly
supposed.
Kepler's second law of planetary motion states that the radius vector connecting a planet to the sun sweeps out equal areas in equal time intervals. In the approximation in which planetary orbits are represented as eccentric circles, this law implies that a typical planet revolves around the sun at a non-uniform rate. However, it is easily demonstrated that the non-uniform rotation of the radius vector connecting the planet to the sun implies a uniform rotation of the radius vector connecting the planet to the so-called equant: i.e., the point directly opposite the sun relative to the geometric center of the orbit--see Fig. 1. Ptolemy discovered the equant scheme empirically, and used it to control the non-uniform rotation of the planets in his model. In fact, this discovery is one of Ptolemy's main claims to fame.
It follows, from the above discussion, that the geocentric model of Ptolemy is equivalent to a heliocentric model in which the various planetary orbits are represented as eccentric circles, and in which the radius vector connecting a given planet to its corresponding equant revolves at a uniform rate. In fact, Ptolemy's model of planetary motion can be thought of as a version of Kepler's model which is accurate to first-order in the planetary eccentricities--see Cha. 4. According to the Ptolemaic scheme, from the point of view of the earth, the orbit of the sun is described by a single circular motion, whereas that of a planet is described by a combination of two circular motions. In reality, the single circular motion of the sun represents the (approximately) circular motion of the earth around the sun, whereas the two circular motions of a typical planet represent a combination of the planet's (approximately) circular motion around the sun, and the earth's motion around the sun. Incidentally, the popular myth that Ptolemy's scheme requires an absurdly large number of circles in order to fit the observational data to any degree of accuracy has no basis in fact. Actually, Ptolemy's model of the sun and the planets, which fits the data very well, only contains 12 circles (i.e., 6 deferents and 6 epicycles).
Ptolemy is often accused of slavish adherence to the tenants of Aristotelian philosophy, to the overall detriment of his model. However, despite Ptolemy's conventional geocentrism, his model of the solar system deviates from orthodox Aristotelism in a number of crucially important respects. First of all, Aristotle argued--from a purely philosophical standpoint--that heavenly bodies should move in single uniform circles. However, in the Ptolemaic system, the motion of the planets is a combination of two circular motions. Moreover, at least one of these motions is non-uniform. Secondly, Aristotle also argued--again from purely philosophical grounds--that the earth is located at the exact center of the universe, about which all heavenly bodies orbit in concentric circles. However, in the Ptolemaic system, the earth is slightly displaced from the center of the universe. Indeed, there is no unique center of the universe, since the circular orbit of the sun and the circular planetary deferents all have slightly different geometric centers, none of which coincide with the earth. As described in the Almagest, the non-orthodox (from the point of view of Aristolelian philosophy) aspects of Ptolemy's model were ultimately dictated by observations. This suggests that, although Ptolemy's world-view was based on Aristolelian philosophy, he did not hesitate to deviate from this standpoint when required to by observational data.
From our heliocentric point of view, it is easily appreciated that the epicycles of the superior planets (i.e., the planets further from the sun than the earth) in Ptolemy's model actually represent the earth's orbit around the sun, whereas the deferents represent the planets' orbits around the sun--see Fig. 29. It follows that the epicycles of the superior planets should all be the same size (i.e., the size of the earth's orbit), and that the radius vectors connecting the centers of the epicycles to the planets should always all point in the same direction as the vector connecting the earth to the sun.
We can also appreciate that the deferents of the inferior planets (i.e., the planets closer to the sun than the earth) in Ptolemy's model actually represent the earth's orbit around the sun, whereas the epicycles represent the planets' orbits around the sun--see Fig. 33. It follows that the deferents of the inferior planets should all be the same size (i.e., the size of the earth's orbit), and that the centers of the epicycles (relative to the earth) should all correspond to the position of the sun (relative to the earth).
 |
The geocentric model of the solar system outlined above represents a perfected version of Ptolemy's model, constructed with a knowledge of the true motions of the planets around the sun. Not surprisingly, the model actually described in the Almagest deviates somewhat from this ideal form. In the following, we shall refer to these deviations as ``errors'', but this should not be understood in a perjorative sense.
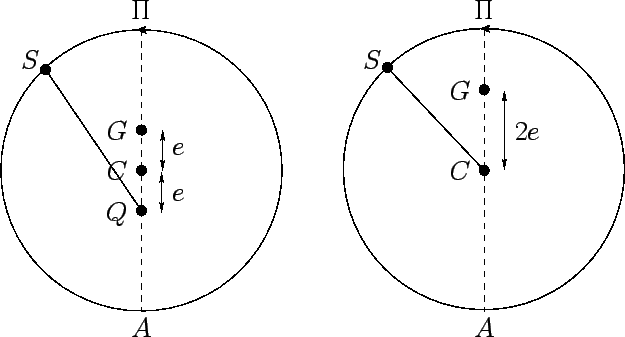
Ptolemy's first error lies in his model of the sun's apparent motion around the earth, which he inherited
from Hipparchus. Figure 1 compares what Ptolemy actually
did, in this respect, compared to
what he should have done in order to be completely consistent
with the rest of his model. Let us normalize the mean radius of the sun's
apparent orbit to unity, for the sake of clarity.
Ptolemy should
have adopted the model shown on the left in Fig. 1, in which the earth
is displaced from the center of the sun's orbit a distance ![]() (the eccentricity of the earth's orbit around the sun) towards the perigee (the point of the sun's closest approach
to the earth), and the equant is displaced the same distance in the opposite
direction. The instantaneous angular position of the sun is then obtained
by allowing the radius vector connecting the equant to the sun to rotate uniformly at the sun's mean orbital angular velocity. Of course, this implies that the
sun rotates non-uniformly about the earth. Ptolemy actually adopted the Hipparchian model
shown on the right in Fig. 1. In this model, the earth is displaced
a distance
(the eccentricity of the earth's orbit around the sun) towards the perigee (the point of the sun's closest approach
to the earth), and the equant is displaced the same distance in the opposite
direction. The instantaneous angular position of the sun is then obtained
by allowing the radius vector connecting the equant to the sun to rotate uniformly at the sun's mean orbital angular velocity. Of course, this implies that the
sun rotates non-uniformly about the earth. Ptolemy actually adopted the Hipparchian model
shown on the right in Fig. 1. In this model, the earth is displaced
a distance ![]() from the center of the sun's orbit in the direction of the perigee,
and the sun rotates at a uniform rate (i.e., the radius vector
from the center of the sun's orbit in the direction of the perigee,
and the sun rotates at a uniform rate (i.e., the radius vector ![]() rotates uniformly). It turns out that, to first-order in
rotates uniformly). It turns out that, to first-order in ![]() , these two
models are equivalent in terms of their ability to predict the angular position of the sun relative to the earth--see Cha. 4. Nevertheless, the Hippachian
model is incorrect, since it predicts too large (by a factor of
, these two
models are equivalent in terms of their ability to predict the angular position of the sun relative to the earth--see Cha. 4. Nevertheless, the Hippachian
model is incorrect, since it predicts too large (by a factor of ![]() ) a variation in the radial distance of the sun from the earth (and, hence, the angular size of the sun) during the
course of a year (see Cha. 4). Ptolemy probabaly adopted
the Hipparchian model because his Aristotelian leanings prejudiced him in favor of uniform circular motion whenever this was consistent with observations.
(It should be noted that Ptolemy was not interested in explaining the relatively small variations in the angular size of the sun during the year--presumably, because this effect was difficult for him to accurately measure.)
) a variation in the radial distance of the sun from the earth (and, hence, the angular size of the sun) during the
course of a year (see Cha. 4). Ptolemy probabaly adopted
the Hipparchian model because his Aristotelian leanings prejudiced him in favor of uniform circular motion whenever this was consistent with observations.
(It should be noted that Ptolemy was not interested in explaining the relatively small variations in the angular size of the sun during the year--presumably, because this effect was difficult for him to accurately measure.)
Ptolemy's next error was to neglect the non-uniform rotation of the superior planets on their epicycles. This is equivalent to neglecting the orbital eccentricity of the earth (recall that the epicycles of the superior planets actually represent the earth's orbit) compared to those of the superior planets. It turns out that this is a fairly good approximation, since the superior planets all have significantly greater orbital eccentricities than the earth. Nevertheless, neglecting the non-uniform rotation of the superior planets on their epicycles has the unfortunate effect of obscuring the tight coupling between the apparent motions of these planets, and that of the sun. The radius vectors connecting the epicycle centers of the superior planets to the planets themselves should always all point exactly in the same direction as that of the sun relative to the earth. When the aforementioned non-uniform rotation is neglected, the radius vectors instead point in the direction of the mean sun relative to the earth. The mean sun is a fictitious body which has the same apparent orbit around the earth as the real sun, but which circles the earth at a uniform rate. The mean sun only coincides with the real sun twice a year.
Ptolemy's third error is associated with his treatment of the inferior planets. As we have seen, in going from the superior to the inferior planets, deferents and epicycles effectively swap roles. For instance, it is the deferents of the inferior planets, rather than the epicycles, which represent the earth's orbit. Hence, for the sake of consistency with his treatment of the superior planets, Ptolemy should have neglected the non-uniform rotation of the epicycle centers around the deferents of the inferior planets, and retained the non-uniform rotation of the planets themselves around the epicycle centers. Instead, he did exactly the opposite. This is equivalent to neglecting the inferior planets' orbital eccentricities relative to that of the earth. It follows that this approximation only works when an inferior planet has a significantly smaller orbital eccentricity than that of the earth. It turns out that this is indeed the case for Venus, which has the smallest eccentricity of any planet in the solar system. Thus, Ptolemy was able to successfully account for the apparent motion of Venus. Mercury, on the other hand, has a much larger orbital eccentricity than the earth. Moreover, it is particularly difficult to obtain good naked-eye positional data for Mercury, since this planet always appears very close to the sun in the sky. Consequently, Ptolemy's Mercury data was highly inaccurate. Not surprisingly, then, Ptolemy was not able to account for the apparent motion of Mercury using his standard deferent-epicycle approach. Instead, in order to fit the data, he was forced to introduce an additional, and quite spurious, epicycle into his model of Mercury's orbit.
Ptolemy's fourth, and possibly largest, error is associated with his treatment of the moon. It should be noted that the moon's motion around the earth is extremely complicated in nature, and was not fully understood until the early 20th century CE. Ptolemy constructed an ingenious geometric model of the moon's orbit which was capable of predicting the lunar ecliptic longitude to reasonable accuracy. Unfortunately, this model necessitates a monthly variation in the earth-moon distance by a factor of about two, which implies a similarly large variation in the moon's angular diameter. However, the observed variation in the moon's diameter is much smaller than this. Hence, Ptolemy's model is not even approximately correct.
Ptolemy's fifth error is associated with his treatment of planetary ecliptic latitudes. Given that the deferents and epicycles of the superior planets represent the orbits of the planets themselves around the sun, and the sun's apparent orbit around the earth, respectively, it follows that one should take the slight inclination of planetary orbits to the ecliptic plane (i.e., the plane of the sun's apparent orbit) into account by tilting the deferents of superior planets, whilst keeping their epicycles parallel to the ecliptic. Similarly, given that the epicycles and deferents of inferior planets represent the orbits of the planets themselves around the sun, and the sun's apparent orbit around the earth, respectively, one should tilt the epicycles of inferior planets, whilst keeping their deferents parallel to the ecliptic. Finally, since the inclination of planetary orbits are all essentially constant in time, the inclinations of the epicycles and deferents should also be constant. Unfortunately, when Ptolemy constructed his theory of planetary latitudes he tilted the both deferents and epicyles of all the planets. Even worse, he allowed the inclinations of the epicycles to the ecliptic plane to vary in time. The net result is a theory which is far more complicated than is necessary.
The final failing in Ptolemy's model of the solar system lies in its scale invariance. Using angular position data alone, Ptolemy was able to determine the ratio of the epicycle radius to that of the deferent for each planet, but was not able to determine the relative sizes of the deferents of different planets. In order to break this scale invariance it is necessary to make an additional assumption--i.e., that the earth orbits the sun. This brings us to Copernicus.