


Next: Mars
Up: The Superior Planets
Previous: The Superior Planets
Figure 29 compares and contrasts heliocentric and geocentric
models of the
motion of a superior planet (i.e., a planet which is further from the
sun than the earth), 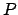 , as seen from the earth,
, as seen from the earth, 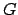 . The sun is
at
. The sun is
at 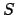 . In the heliocentric
model, we can write the earth-planet displacement vector,
. In the heliocentric
model, we can write the earth-planet displacement vector, 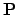 ,
as the sum of the earth-sun displacement vector,
,
as the sum of the earth-sun displacement vector,  , and
the sun-planet displacement vector,
, and
the sun-planet displacement vector,  . The geocentric model,
which is entirely equivalent to the heliocentric model as far as
the relative motion of the planet with respect to the
earth is concerned, and is much more convenient, relies on the simple vector identity
. The geocentric model,
which is entirely equivalent to the heliocentric model as far as
the relative motion of the planet with respect to the
earth is concerned, and is much more convenient, relies on the simple vector identity
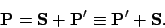 |
(155) |
In other words, we can get from the earth to the planet by one of two
different routes. The first route corresponds to the heliocentric model, and
the second to the geocentric model.
In the latter model,  gives the displacement of
the so-called guide-point,
gives the displacement of
the so-called guide-point, 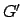 , from the earth.
Since
, from the earth.
Since  is also the displacement of the planet,
is also the displacement of the planet, 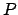 , from the
sun,
, from the
sun, 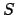 , it is clear that
, it is clear that 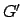 executes a
Keplerian orbit about the earth whose elements are the
same as those of the orbit of the planet about the sun.
The ellipse traced out by
executes a
Keplerian orbit about the earth whose elements are the
same as those of the orbit of the planet about the sun.
The ellipse traced out by 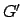 is termed the deferent. The vector
is termed the deferent. The vector  gives
the displacement of the planet from the guide-point.
However,
gives
the displacement of the planet from the guide-point.
However,  is also the displacement of the sun from the earth.
Hence, it is clear that the planet,
is also the displacement of the sun from the earth.
Hence, it is clear that the planet, 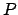 ,
executes a Keplerian orbit about the guide-point,
,
executes a Keplerian orbit about the guide-point, 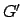 , whose
elements are the same as the sun's apparent orbit about the earth.
The ellipse traced out by
, whose
elements are the same as the sun's apparent orbit about the earth.
The ellipse traced out by 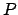 about
about 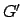 is termed the epicycle.
is termed the epicycle.
Figure 29:
Heliocentric and geocentric models of the motion of a superior planet. Here, 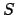 is the sun,
is the sun, 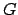 the earth, and
the earth, and 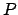 the planet. View is from the northern ecliptic pole.
the planet. View is from the northern ecliptic pole.
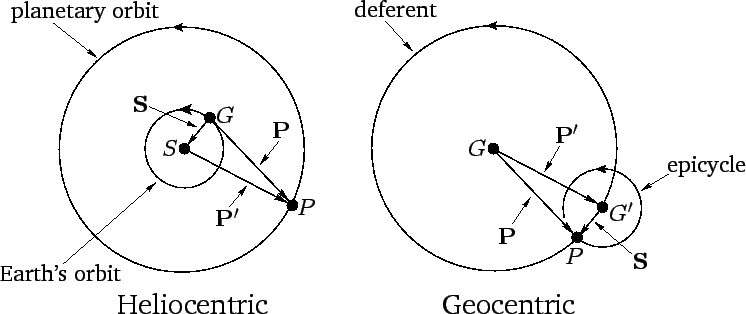 |
Figure 30:
Planetary longitude model. View is from northern ecliptic pole.
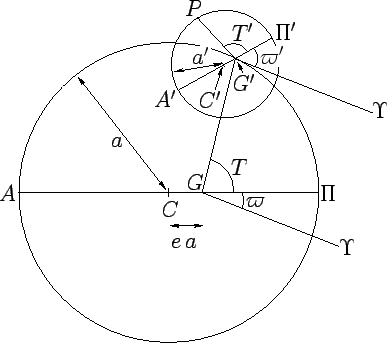 |
Figure 30 illustrates in more detail how the deferent-epicycle model
is used to determine the ecliptic longitude of a superior planet.
The planet 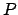 orbits (counterclockwise) on a small Keplerian orbit
orbits (counterclockwise) on a small Keplerian orbit 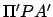 about guide-point
about guide-point 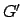 , which, in turn, orbits the earth,
, which, in turn, orbits the earth, 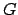 , (counterclockwise) on a large
Keplerian orbit
, (counterclockwise) on a large
Keplerian orbit  . As has already been mentioned, the small orbit is termed the epicycle, and the large orbit the deferent. Both orbits are assumed to lie in the plane of the ecliptic. This approximation does not
introduce a large error into our calculations because the orbital inclinations of the visible planets to
the ecliptic plane are all fairly small.
Let
. As has already been mentioned, the small orbit is termed the epicycle, and the large orbit the deferent. Both orbits are assumed to lie in the plane of the ecliptic. This approximation does not
introduce a large error into our calculations because the orbital inclinations of the visible planets to
the ecliptic plane are all fairly small.
Let 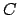 ,
, 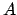 ,
, 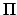 ,
, 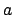 ,
, 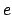 ,
, 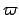 ,
and
,
and  denote the geometric center, apocenter (i.e., the point of
furthest distance from the central object), pericenter (i.e., the
point of closest approach to the central object), major radius, eccentricity, longitude
of the pericenter, and true anomaly of the deferent, respectively. Let
denote the geometric center, apocenter (i.e., the point of
furthest distance from the central object), pericenter (i.e., the
point of closest approach to the central object), major radius, eccentricity, longitude
of the pericenter, and true anomaly of the deferent, respectively. Let 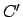 ,
, 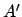 ,
, 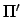 ,
,  ,
, 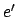 ,
, 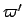 , and
, and  denote the corresponding
quantities for the epicycle.
denote the corresponding
quantities for the epicycle.
Figure 31:
The triangle  .
.
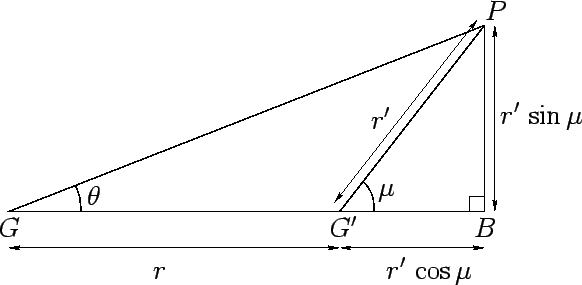 |
Let the line 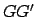 be produced, and let the perpendicular
be produced, and let the perpendicular 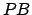 be
dropped to it from
be
dropped to it from 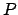 , as shown in Fig. 31. The angle
, as shown in Fig. 31. The angle
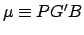 is termed the epicyclic anomaly (see Fig. 32), and takes the form
is termed the epicyclic anomaly (see Fig. 32), and takes the form
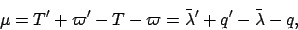 |
(156) |
where 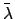 and
and 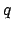 are the mean longitude and equation of center for the
deferent, whereas
are the mean longitude and equation of center for the
deferent, whereas
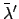 and
and 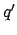 are the corresponding quantities for the
epicycle--see Cha. 5. The epicyclic anomaly is generally written in the
range
are the corresponding quantities for the
epicycle--see Cha. 5. The epicyclic anomaly is generally written in the
range 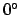 to
to  .
The angle
.
The angle
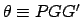 is termed the equation of the epicycle, and is usually written in the range
is termed the equation of the epicycle, and is usually written in the range  to
to 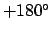 .
It is clear from the figure that
.
It is clear from the figure that
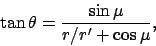 |
(157) |
where 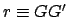 and
and 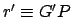 are the radial polar coordinates for the deferent and epicycle,
respectively.
Moreover, according to Equation (81),
are the radial polar coordinates for the deferent and epicycle,
respectively.
Moreover, according to Equation (81),
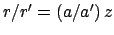 , where
, where
 |
(158) |
and
are termed radial anomalies.
Finally, the ecliptic longitude of the planet is given by (see Fig. 32)
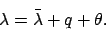 |
(161) |
Now,
![\begin{displaymath}
\theta(\mu,z) \equiv \tan^{-1}\left[ \frac{\sin\mu}{(a/a')\,z+ \cos\mu}\right]
\end{displaymath}](img1673.png) |
(162) |
is a function of two variables, 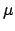 and
and 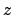 . It is impractical to tabulate
such a function directly. Fortunately, whilst
. It is impractical to tabulate
such a function directly. Fortunately, whilst 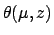 has a strong dependence on
has a strong dependence on 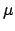 , it only has a fairly weak dependence on
, it only has a fairly weak dependence on 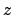 .
In fact, it is easily seen that
.
In fact, it is easily seen that 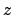 varies between
varies between
 and
and
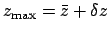 , where
, where
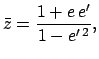 |
|
|
(163) |
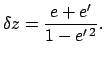 |
|
|
(164) |
Let us define
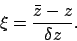 |
(165) |
This variable takes the value 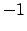 when
when 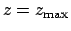 , the value
, the value 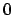 when
when
 , and the value
, and the value  when
when 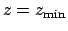 .
Thus, using quadratic interpolation, we can write
.
Thus, using quadratic interpolation, we can write
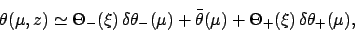 |
(166) |
where
and
This scheme allows us to avoid having to tabulate a
two-dimensional function, whilst ensuring that the exact value of 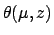 is obtained
when
is obtained
when  ,
, 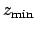 , or
, or 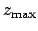 . The above interpolation
scheme is very similar to that adopted by Ptolemy in the Almagest.
. The above interpolation
scheme is very similar to that adopted by Ptolemy in the Almagest.
Our procedure for determining the ecliptic longitude of a superior planet is described below. It is assumed that the ecliptic longitude, 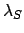 , and the
radial anomaly,
, and the
radial anomaly, 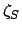 , of the sun have already been calculated. The latter quantity is tabulated as a function of the solar mean anomaly
in Table 33. In the following,
, of the sun have already been calculated. The latter quantity is tabulated as a function of the solar mean anomaly
in Table 33. In the following, 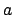 ,
, 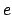 ,
, 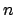 ,
,  ,
,
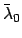 , and
, and 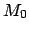 represent elements of the orbit of the planet in question
about the sun, and
represent elements of the orbit of the planet in question
about the sun, and 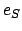 represents the eccentricity of the sun's apparent orbit
about the earth. (In general, the subscript
represents the eccentricity of the sun's apparent orbit
about the earth. (In general, the subscript 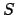 denotes the sun.) In particular,
denotes the sun.) In particular, 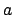 is the major radius of the planetary orbit in
units in which the major radius of the sun's apparent orbit about the
earth is unity. The requisite elements for all of the superior planets at the J2000 epoch (
is the major radius of the planetary orbit in
units in which the major radius of the sun's apparent orbit about the
earth is unity. The requisite elements for all of the superior planets at the J2000 epoch (
 JD)
are listed in Table 30. The ecliptic longitude of a superior
planet is specified by the following formulae:
JD)
are listed in Table 30. The ecliptic longitude of a superior
planet is specified by the following formulae:
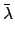 |
 |
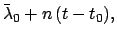 |
(172) |
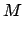 |
 |
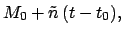 |
(173) |
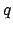 |
 |
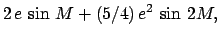 |
(174) |
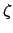 |
 |
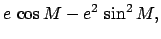 |
(175) |
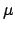 |
 |
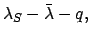 |
(176) |
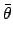 |
 |
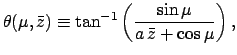 |
(177) |
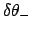 |
 |
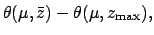 |
(178) |
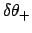 |
 |
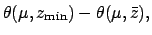 |
(179) |
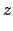 |
 |
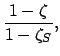 |
(180) |
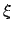 |
 |
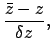 |
(181) |
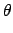 |
 |
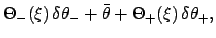 |
(182) |
 |
 |
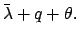 |
(183) |
Here,
 ,
,
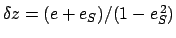 ,
,
 ,
and
,
and
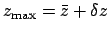 . The constants
. The constants 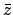 ,
,  ,
, 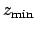 , and
, and 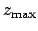 for each of the superior planets are listed in Table 44. Finally, the functions
for each of the superior planets are listed in Table 44. Finally, the functions  are tabulated in Table 45.
are tabulated in Table 45.
For the case of Mars, the above formulae are capable of matching NASA ephemeris data during the years 1995-2006 CE
with a mean error of  and a maximum error of
and a maximum error of 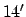 . For the case of Jupiter, the mean error is
. For the case of Jupiter, the mean error is
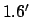 and the maximum error
and the maximum error 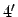 . Finally, for the case of Saturn, the mean error is
. Finally, for the case of Saturn, the mean error is 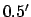 and the
maximum error
and the
maximum error 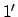 .
.



Next: Mars
Up: The Superior Planets
Previous: The Superior Planets
Richard Fitzpatrick
2010-07-21

![]() orbits (counterclockwise) on a small Keplerian orbit
orbits (counterclockwise) on a small Keplerian orbit ![]() about guide-point
about guide-point ![]() , which, in turn, orbits the earth,
, which, in turn, orbits the earth, ![]() , (counterclockwise) on a large
Keplerian orbit
, (counterclockwise) on a large
Keplerian orbit ![]() . As has already been mentioned, the small orbit is termed the epicycle, and the large orbit the deferent. Both orbits are assumed to lie in the plane of the ecliptic. This approximation does not
introduce a large error into our calculations because the orbital inclinations of the visible planets to
the ecliptic plane are all fairly small.
Let
. As has already been mentioned, the small orbit is termed the epicycle, and the large orbit the deferent. Both orbits are assumed to lie in the plane of the ecliptic. This approximation does not
introduce a large error into our calculations because the orbital inclinations of the visible planets to
the ecliptic plane are all fairly small.
Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() denote the geometric center, apocenter (i.e., the point of
furthest distance from the central object), pericenter (i.e., the
point of closest approach to the central object), major radius, eccentricity, longitude
of the pericenter, and true anomaly of the deferent, respectively. Let
denote the geometric center, apocenter (i.e., the point of
furthest distance from the central object), pericenter (i.e., the
point of closest approach to the central object), major radius, eccentricity, longitude
of the pericenter, and true anomaly of the deferent, respectively. Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote the corresponding
quantities for the epicycle.
denote the corresponding
quantities for the epicycle.
![]() be produced, and let the perpendicular
be produced, and let the perpendicular ![]() be
dropped to it from
be
dropped to it from ![]() , as shown in Fig. 31. The angle
, as shown in Fig. 31. The angle
![]() is termed the epicyclic anomaly (see Fig. 32), and takes the form
is termed the epicyclic anomaly (see Fig. 32), and takes the form
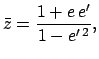
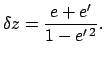
![]() , and the
radial anomaly,
, and the
radial anomaly, ![]() , of the sun have already been calculated. The latter quantity is tabulated as a function of the solar mean anomaly
in Table 33. In the following,
, of the sun have already been calculated. The latter quantity is tabulated as a function of the solar mean anomaly
in Table 33. In the following, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and ![]() represent elements of the orbit of the planet in question
about the sun, and
represent elements of the orbit of the planet in question
about the sun, and ![]() represents the eccentricity of the sun's apparent orbit
about the earth. (In general, the subscript
represents the eccentricity of the sun's apparent orbit
about the earth. (In general, the subscript ![]() denotes the sun.) In particular,
denotes the sun.) In particular, ![]() is the major radius of the planetary orbit in
units in which the major radius of the sun's apparent orbit about the
earth is unity. The requisite elements for all of the superior planets at the J2000 epoch (
is the major radius of the planetary orbit in
units in which the major radius of the sun's apparent orbit about the
earth is unity. The requisite elements for all of the superior planets at the J2000 epoch (
![]() JD)
are listed in Table 30. The ecliptic longitude of a superior
planet is specified by the following formulae:
JD)
are listed in Table 30. The ecliptic longitude of a superior
planet is specified by the following formulae:
![]() and a maximum error of
and a maximum error of ![]() . For the case of Jupiter, the mean error is
. For the case of Jupiter, the mean error is
![]() and the maximum error
and the maximum error ![]() . Finally, for the case of Saturn, the mean error is
. Finally, for the case of Saturn, the mean error is ![]() and the
maximum error
and the
maximum error ![]() .
.