

Next: Mean values
Up: Applications of statistical thermodynamics
Previous: Boltzmann distributions
The simplest microscopic system which we can analyze using the Boltzmann distribution
is one
which has only two possible states (there would clearly be little point in analyzing
a system with only one possible state). Most elements, and some compounds, are
paramagnetic: i.e., their constituent atoms, or molecules,
possess a permanent
magnetic moment due to the presence of one or more unpaired electrons. Consider a
substance whose constituent
particles contain only one unpaired electron. Such particles have spin
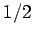 , and consequently possess an intrinsic magnetic moment
, and consequently possess an intrinsic magnetic moment 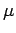 .
According to quantum mechanics, the magnetic moment of a spin
.
According to quantum mechanics, the magnetic moment of a spin 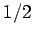 particle
can
point either parallel or antiparallel to an external magnetic field
particle
can
point either parallel or antiparallel to an external magnetic field 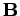 .
Let us determine the mean magnetic moment
.
Let us determine the mean magnetic moment
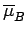 (in the direction
of
(in the direction
of 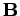 ) of the constituent particles of
the substance when its absolute temperature is
) of the constituent particles of
the substance when its absolute temperature is 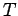 .
We assume, for the sake of simplicity, that each atom (or molecule)
only interacts weakly
with its neighbouring atoms. This enables us to focus attention on a single atom, and
treat the remaining atoms as a heat bath at temperature
.
We assume, for the sake of simplicity, that each atom (or molecule)
only interacts weakly
with its neighbouring atoms. This enables us to focus attention on a single atom, and
treat the remaining atoms as a heat bath at temperature 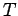 .
.
Our atom can be in one of two possible states: the 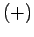 state in which its spin
points up (i.e., parallel to
state in which its spin
points up (i.e., parallel to 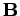 ), and the
), and the 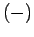 state in which its
spin points down (i.e., antiparallel to
state in which its
spin points down (i.e., antiparallel to 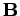 ). In the
). In the 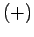 state,
the atomic magnetic moment is parallel to the magnetic field, so that
state,
the atomic magnetic moment is parallel to the magnetic field, so that
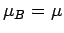 . The magnetic energy of the atom is
. The magnetic energy of the atom is
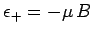 .
In the
.
In the 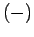 state, the atomic magnetic moment is antiparallel to the magnetic
field, so that
state, the atomic magnetic moment is antiparallel to the magnetic
field, so that 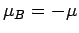 . The magnetic energy of the atom is
. The magnetic energy of the atom is
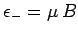 .
.
According to the Boltzmann distribution, the probability of finding the atom
in the 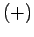 state is
state is
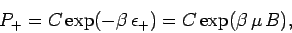 |
(381) |
where 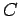 is a constant, and
is a constant, and
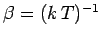 .
Likewise, the probability of finding the atom in the
.
Likewise, the probability of finding the atom in the 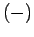 state is
state is
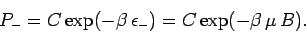 |
(382) |
Clearly, the most probable
state is the state with the lowest energy [i.e., the 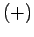 state].
Thus, the mean magnetic moment points in the direction of the magnetic field
(i.e., the atom is more likely to point parallel to the field than antiparallel).
state].
Thus, the mean magnetic moment points in the direction of the magnetic field
(i.e., the atom is more likely to point parallel to the field than antiparallel).
It is clear that the critical parameter in a paramagnetic system is
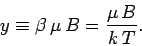 |
(383) |
This parameter measures the ratio of the typical magnetic energy of the atom to
its typical thermal energy. If the thermal energy greatly exceeds the magnetic
energy then 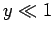 , and the probability that the atomic moment points parallel
to the magnetic field is about the same as the probability that it points
antiparallel. In this situation, we expect the mean atomic moment to
be small, so that
, and the probability that the atomic moment points parallel
to the magnetic field is about the same as the probability that it points
antiparallel. In this situation, we expect the mean atomic moment to
be small, so that
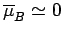 . On the other hand, if the
magnetic energy greatly exceeds the thermal energy then
. On the other hand, if the
magnetic energy greatly exceeds the thermal energy then 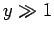 , and the atomic
moment is far more likely to point parallel to the magnetic field than antiparallel.
In this situation, we expect
, and the atomic
moment is far more likely to point parallel to the magnetic field than antiparallel.
In this situation, we expect
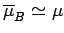 .
.
Let us calculate the mean atomic moment
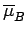 . The usual
definition of a mean value gives
. The usual
definition of a mean value gives
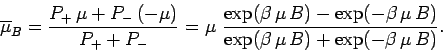 |
(384) |
This can also be written
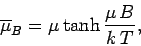 |
(385) |
where the hyperbolic tangent is defined
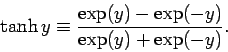 |
(386) |
For small arguments, 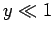 ,
,
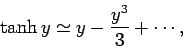 |
(387) |
whereas for large arguments, 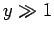 ,
,
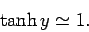 |
(388) |
It follows that at comparatively high temperatures,
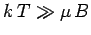 ,
,
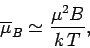 |
(389) |
whereas at comparatively low temperatures,
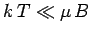 ,
,
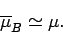 |
(390) |
Suppose that the substance contains 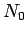 atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by
atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by
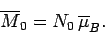 |
(391) |
At high temperatures,
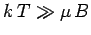 , the mean magnetic moment, and, hence, the
magnetization, is proportional to the applied magnetic field, so we can write
, the mean magnetic moment, and, hence, the
magnetization, is proportional to the applied magnetic field, so we can write
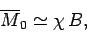 |
(392) |
where 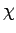 is a constant of proportionality known as the
magnetic susceptibility.
It is clear that the magnetic susceptibility of a spin 1/2 paramagnetic substance
takes the form
is a constant of proportionality known as the
magnetic susceptibility.
It is clear that the magnetic susceptibility of a spin 1/2 paramagnetic substance
takes the form
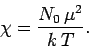 |
(393) |
The fact that
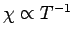 is known as Curie's law, because it
was discovered experimentally by Pierre Curie at the end of the nineteenth century.
At low temperatures,
is known as Curie's law, because it
was discovered experimentally by Pierre Curie at the end of the nineteenth century.
At low temperatures,
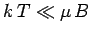 ,
,
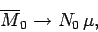 |
(394) |
so the magnetization becomes independent of the applied field. This corresponds to
the maximum possible magnetization, where all atomic moments are lined up
parallel to the field. The breakdown of the
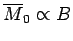 law
at low temperatures (or high magnetic fields) is known as saturation.
law
at low temperatures (or high magnetic fields) is known as saturation.
Figure 2:
The magnetization (vertical axis) versus 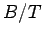 (horizontal axis) curves
for (I) chromium potassium alum (
(horizontal axis) curves
for (I) chromium potassium alum (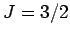 ), (II) iron ammonium alum (
), (II) iron ammonium alum (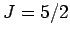 ), and
(III) gadolinium sulphate (
), and
(III) gadolinium sulphate (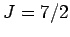 ). The solid lines are the theoretical predictions
whereas
the data points are experimental measurements. From W.E. Henry, Phys. Rev. 88, 561 (1952).
). The solid lines are the theoretical predictions
whereas
the data points are experimental measurements. From W.E. Henry, Phys. Rev. 88, 561 (1952).
 |
The above analysis is only valid for paramagnetic substances made up of
spin one-half (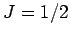 ) atoms or molecules. However,
the analysis can easily be generalized
to take account of substances whose constituent particles possess higher spin
(i.e.,
) atoms or molecules. However,
the analysis can easily be generalized
to take account of substances whose constituent particles possess higher spin
(i.e., 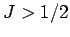 ). Figure 2 compares
the experimental and theoretical magnetization versus
field-strength curves for three different substances made up of spin
). Figure 2 compares
the experimental and theoretical magnetization versus
field-strength curves for three different substances made up of spin 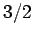 , spin
, spin 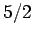 ,
and spin
,
and spin 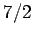 particles, showing the excellent agreement between the two sets of
curves. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.
particles, showing the excellent agreement between the two sets of
curves. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.
The previous analysis completely neglects any interaction between the
spins of neighbouring atoms or molecules. It turns out that this is
a fairly good approximation for paramagnetic substances. However, for
ferromagnetic substances, in which the spins of neighbouring atoms
interact very strongly, this approximation breaks down completely. Thus, the
above analysis does not apply to ferromagnetic substances.


Next: Mean values
Up: Applications of statistical thermodynamics
Previous: Boltzmann distributions
Richard Fitzpatrick
2006-02-02
![]() state in which its spin
points up (i.e., parallel to
state in which its spin
points up (i.e., parallel to ![]() ), and the
), and the ![]() state in which its
spin points down (i.e., antiparallel to
state in which its
spin points down (i.e., antiparallel to ![]() ). In the
). In the ![]() state,
the atomic magnetic moment is parallel to the magnetic field, so that
state,
the atomic magnetic moment is parallel to the magnetic field, so that
![]() . The magnetic energy of the atom is
. The magnetic energy of the atom is
![]() .
In the
.
In the ![]() state, the atomic magnetic moment is antiparallel to the magnetic
field, so that
state, the atomic magnetic moment is antiparallel to the magnetic
field, so that ![]() . The magnetic energy of the atom is
. The magnetic energy of the atom is
![]() .
.
![]() state is
state is
![]() . The usual
definition of a mean value gives
. The usual
definition of a mean value gives
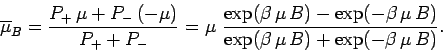
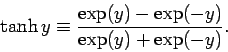
![]() atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by
atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by

![]() ) atoms or molecules. However,
the analysis can easily be generalized
to take account of substances whose constituent particles possess higher spin
(i.e.,
) atoms or molecules. However,
the analysis can easily be generalized
to take account of substances whose constituent particles possess higher spin
(i.e., ![]() ). Figure 2 compares
the experimental and theoretical magnetization versus
field-strength curves for three different substances made up of spin
). Figure 2 compares
the experimental and theoretical magnetization versus
field-strength curves for three different substances made up of spin ![]() , spin
, spin ![]() ,
and spin
,
and spin ![]() particles, showing the excellent agreement between the two sets of
curves. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.
particles, showing the excellent agreement between the two sets of
curves. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.