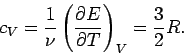Calculation of specific heats

Now that we know the relationship between the specific heats at constant volume and constant pressure for an ideal gas, it would be nice if we could calculate either one of these quantities from first principles. Classical thermodynamics cannot help us here. However, it is quite easy to calculate the specific heat at constant volume using our knowledge of statistical physics. Recall, that the variation of the number of accessible states of an ideal gas with energy and volume is written

$${\mit\Omega}(E, V) \propto V^N \chi(E).$$ (301)

For the specific case of a monatomic ideal gas, we worked out a more exact expression for ${\mit\Omega}$ in Sect. 3.8: i.e.,

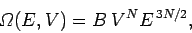$${\mit\Omega}(E, V) = B\,V^N E^{\,3N/2},$$ (302)

where 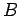$B$ is a constant independent of the energy and volume. It follows that

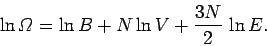$$\ln {\mit\Omega} = \ln B + N\ln V +\frac{3N}{2}\, \ln E.$$ (303)

The temperature is given by

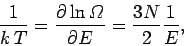$$\frac{1}{k\,T} = \frac{\partial \ln{\mit\Omega}}{\partial E} = \frac{3N}{2} \frac{1}{E},$$ (304)

so

$$E = \frac{3}{2}\, N \,k\,T.$$ (305)

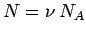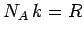Since, $N= \nu \,N_A$, and $N_A \,k=R$, we can rewrite the above expression as

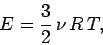$$E = \frac{3}{2}\, \nu\, R\,T,$$ (306)

where 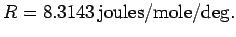$R= 8.3143\,{\rm joules/mole/deg.}$ is the ideal gas constant. The above formula tells us exactly how the internal energy of a monatomic ideal gas depends on its temperature.

The molar specific heat at constant volume of a monatomic ideal gas is clearly

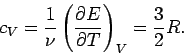$$c_V = \frac{1}{\nu} \left(\frac{\partial E}{\partial T}\right)_V = \frac{3}{2} R.$$ (307)

This has the numerical value

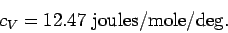$$c_V = 12.47 \,\,{\rm joules/mole/deg.}$$ (308)

Furthermore, we have

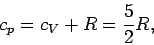$$c_p = c_V + R = \frac{5}{2} R,$$ (309)

and

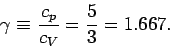$$\gamma \equiv \frac{c_p}{c_V} = \frac{5}{3} = 1.667.$$ (310)

We can see from the previous table that these predictions are borne out pretty well for the monatomic gases Helium and Argon. Note that the specific heats of polyatomic gases are larger than those of monatomic gases. This is because polyatomic molecules can rotate around their centres of mass, as well as translate, so polyatomic gases can store energy in the rotational, as well as the translational, energy states of their constituent particles. We shall analyze this effect in greater detail later on in this course.