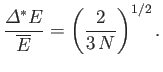Next: Quantum Statistics
Up: Applications of Statistical Thermodynamics
Previous: Ferromagnetism
- Demonstrate that the geometric series
can be summed to give
Here, 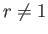 . Hence, deduce that
. Hence, deduce that
assuming that 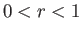 .
.
- Let
Demonstrate that
Furthermore, show that
(see Exercise 2), and
Hence, deduce that
- A sample of mineral oil is placed in an external magnetic field
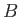 . Each
proton has spin
. Each
proton has spin 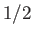 , and a magnetic moment
, and a magnetic moment 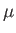 . It can, therefore, have
two possible energies,
. It can, therefore, have
two possible energies,
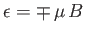 , corresponding to the two possible
orientations of its spin. An applied radio-frequency field can induce transitions
between these two energy levels if its frequency
, corresponding to the two possible
orientations of its spin. An applied radio-frequency field can induce transitions
between these two energy levels if its frequency 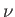 satisfies the Bohr
condition
satisfies the Bohr
condition
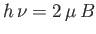 . The power absorbed from this radiation
field is then proportional to the difference in the number of nuclei in these
two energy levels. Assume that the protons in the mineral oil are in thermal
equilibrium at a temperature
. The power absorbed from this radiation
field is then proportional to the difference in the number of nuclei in these
two energy levels. Assume that the protons in the mineral oil are in thermal
equilibrium at a temperature  that is sufficiently high that
that is sufficiently high that
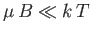 . How
does the absorbed power depend on the temperature,
. How
does the absorbed power depend on the temperature,  , of the sample?
, of the sample?
- Consider an assembly of
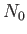 weakly-interacting magnetic atoms per unit volume, held
at temperature
weakly-interacting magnetic atoms per unit volume, held
at temperature  . According to classical physics, each atomic magnetic moment,
. According to classical physics, each atomic magnetic moment,
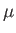 , can
be orientated so as to make an arbitrary angle
, can
be orientated so as to make an arbitrary angle 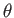 with respect to the
with respect to the 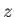 -direction (say).
In the absence of an external magnetic field, the probability that the angle
lies between
-direction (say).
In the absence of an external magnetic field, the probability that the angle
lies between 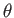 and
and
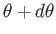 is simply proportional to the solid
angle,
is simply proportional to the solid
angle,
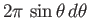 , enclosed in this range. In the presence of
a magnetic field of strength
, enclosed in this range. In the presence of
a magnetic field of strength 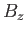 , directed parallel to the
, directed parallel to the 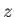 -axis, this probability
is further proportional to the Boltzmann factor,
-axis, this probability
is further proportional to the Boltzmann factor,
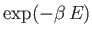 , where
, where
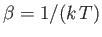 , and
, and
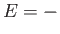
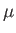
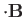 is the magnetic energy of the atom.
is the magnetic energy of the atom.
- Show that the classical mean magnetization is
where
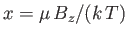 , and
, and
is known as the Langevin function.
- Demonstrate that the corresponding quantum mechanical expression for a collection of
atoms with overall angular momentum
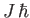 is
is
where
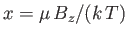 ,
,
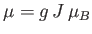 ,
and
,
and
is the Brillouin function.
- Show, finally, that the previous two expressions are identical in the classical limit
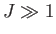 . (This is the classical
limit because the spacing between adjacent magnetic energy levels,
. (This is the classical
limit because the spacing between adjacent magnetic energy levels,
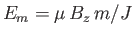 , where
, where 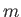 is an integer lying between
is an integer lying between 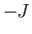 and
and 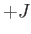 , is
, is
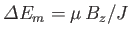 , which tends to zero as
, which tends to zero as
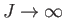 .)
.)
- Consider a spin-1/2 (i.e.,
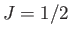 and
and 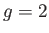 ) paramagnetic substance containing
) paramagnetic substance containing  non-interacting atoms.
non-interacting atoms.
- Show
that the overall magnetic partition function,
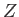 , is such that
, is such that
where 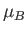 is the Bohr magneton,
is the Bohr magneton, 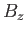 the magnetic field-strength, and
the magnetic field-strength, and  the absolute temperature.
the absolute temperature.
- Demonstrate that the mean magnetic energy of the system is
where
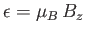 .
Show that
.
Show that
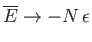 as
as
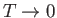 , and
, and
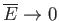 as
as
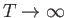 .
Plot
.
Plot
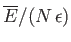 versus
versus
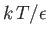 .
.
- Demonstrate that the magnetic contribution to the specific heat of the substance is
and that
when
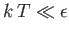 , whereas
, whereas
when
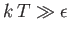 . Plot
. Plot 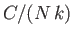 versus
versus
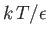 . The sharp peak that is evident when
. The sharp peak that is evident when
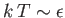 is
known as the Schottky anomaly.
is
known as the Schottky anomaly.
- Show that the magnetic contribution to the entropy
of the substance is
and demonsrate that
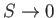 as
as
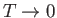 and
and
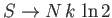 as
as
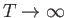 .
Plot
.
Plot 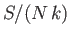 versus
versus
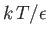 .
.
- The nuclei of atoms in a certain crystalline solid have spin one. According
to quantum theory, each nucleus can therefore be in any one of three quantum states
labeled by the quantum number
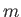 , where
, where 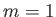 , 0, or
, 0, or 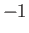 . This quantum number
measures the projection of the nuclear spin along a crystal axis of the solid.
Because the electric charge distribution in the nucleus is not spherically
symmetric, but ellipsoidal, the energy of a nucleus depends on its spin
orientation with respect to the internal electric field existing at its location.
Thus a nucleus has the same energy
. This quantum number
measures the projection of the nuclear spin along a crystal axis of the solid.
Because the electric charge distribution in the nucleus is not spherically
symmetric, but ellipsoidal, the energy of a nucleus depends on its spin
orientation with respect to the internal electric field existing at its location.
Thus a nucleus has the same energy
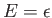 in the state
in the state 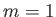 and the state
and the state
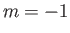 , compared with energy
, compared with energy 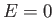 in the state
in the state 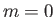 .
.
- Find an expression, as a function of absolute temperature,
 , of the nuclear
contribution to the molar internal energy of the solid.
, of the nuclear
contribution to the molar internal energy of the solid.
- Find an expression, as a function of
 , of the nuclear contribution to
the molar entropy of the solid.
, of the nuclear contribution to
the molar entropy of the solid.
- By directly counting the total number of accessible states, calculate the
nuclear contribution to the molar entropy of the solid at very low temperatures.
Calculate it also at high temperatures. Show that the expression in part (b) reduces
properly to these values as
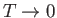 and
and
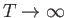 .
.
- Make a qualitative graph showing the temperature dependence of the nuclear
contribution to the molar heat capacity of the solid. Calculate the temperature
dependence explicitly. What is the temperature dependence for large values
of
 ?
?
- A dilute solution of a macromolecule (large molecules of biological
interest) at temperature
 is placed in an ultracentrifuge rotating with
angular velocity
is placed in an ultracentrifuge rotating with
angular velocity 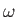 . The centripetal acceleration
. The centripetal acceleration
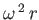 acting on
a particle of mass
acting on
a particle of mass 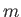 may then be replaced by an equivalent centrifugal
force
may then be replaced by an equivalent centrifugal
force
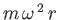 in the rotating frame of reference.
in the rotating frame of reference.
- Find how the relative density,
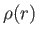 , of molecules varies with their radial
distance,
, of molecules varies with their radial
distance, 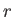 , from the axis of rotation.
, from the axis of rotation.
- Show qualitatively how the molecular weight of the macromolecules can be
determined if the density ratio
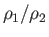 at the radii
at the radii 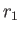 and
and 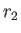 is measured by optical means.
is measured by optical means.
- Consider a homogeneous mixture of inert monatomic ideal gases at absolute
temperature
 in a container of volume
in a container of volume  . Let there be
. Let there be 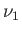 moles of
gas 1,
moles of
gas 1, 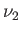 moles of gas 2, ..., and
moles of gas 2, ..., and 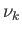 moles of gas
moles of gas 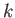 .
.
- By considering the classical partition function of this system,
derive its equation of state. In other words, find an expression for its total
mean pressure,
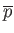 .
.
- How is this total pressure,
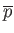 , of the gas related to the so-called
partial pressure,
, of the gas related to the so-called
partial pressure,
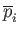 , that the
, that the 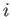 th gas would produce if it alone
occupied the entire volume at this temperature?
th gas would produce if it alone
occupied the entire volume at this temperature?
- Monatomic molecules adsorbed on a surface are free to move on this surface,
and can be treated as a classical ideal two-dimensional gas. At absolute temperature
 , what is the heat capacity per mole of molecules thus adsorbed on a surface of
fixed size?
, what is the heat capacity per mole of molecules thus adsorbed on a surface of
fixed size?
- Consider a system in thermal equilibrium with a heat bath held at absolute temperature
 . The
probability of observing the system in some state
. The
probability of observing the system in some state 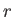 of energy
of energy 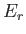 is is given by the canonical
probability distribution:
is is given by the canonical
probability distribution:
where
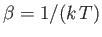 , and
, and
is the partition function.
- Demonstrate that the entropy can be written
- Demonstrate that the mean Helmholtz free energy is related to the partition function according to
- Show that the logarithm of the classical partition function of an ideal gas consisting of
 identical molecules of mass
identical molecules of mass 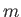 , held in a container of
volume
, held in a container of
volume  , and in thermal equilibrium with a heat bath held at absolute temperature
, and in thermal equilibrium with a heat bath held at absolute temperature  , is
, is
where
Here,
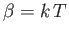 , and
, and 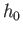 parameterizes how finely classical phase-space is partitioned.
Demonstrate that:
parameterizes how finely classical phase-space is partitioned.
Demonstrate that:
- Use the Debye approximation to calculate the contribution of lattice vibrations to the thermodynamic
functions of a solid.
- To be more specific, show that
Here,  is the number of atoms in the solid,
is the number of atoms in the solid,  the absolute temperature,
the absolute temperature, 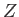 the partition function,
the partition function,
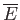 the mean energy,
the mean energy, 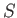 the
entropy,
the
entropy,
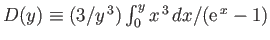 ,
,
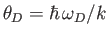 , and
, and 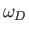 is the Debye frequency.
is the Debye frequency.
- Show that in the limit
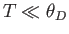 ,
,
[Hint:
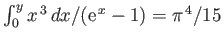 .]
.]
- Show that in the limit
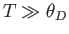 ,
,
- Further, show that
where 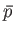 is the mean pressure,
is the mean pressure,  the volume, and
the volume, and
- For the quantized lattice waves (phonons) in the Debye theory of specific heats, the frequency,
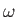 ,
of a propagating wave is related to its wavevector,
,
of a propagating wave is related to its wavevector, 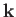 , by the dispersion relation
, by the dispersion relation
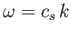 ,
where
,
where 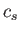 is the velocity of sound. On the other hand, in a ferromagnetic solid at low
temperatures, quantized waves of magnetization (spin waves) have their frequencies,
is the velocity of sound. On the other hand, in a ferromagnetic solid at low
temperatures, quantized waves of magnetization (spin waves) have their frequencies, 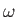 , related
to their wavevectors,
, related
to their wavevectors, 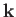 , according to the dispersion relation
, according to the dispersion relation
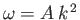 , where
, where
 is a constant. Show that, at low temperatures, the contribution of spin waves to the heat capacity of
the ferromagnet varies as
is a constant. Show that, at low temperatures, the contribution of spin waves to the heat capacity of
the ferromagnet varies as 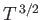 .
.
- Verify directly that
for a Maxwellian velocity distribution. Here, 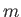 is the molecular mass, and
is the molecular mass, and  the absolute temperature.
the absolute temperature.
- Show that the mean speed of molecules effusing through a small hole in a gas-filled container is
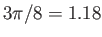 times larger than the
mean speed of the molecules within the container.
times larger than the
mean speed of the molecules within the container.
- A vessel is closed off by a porous partition through which gases can pass by effusion and then be pumped off to some collecting
chamber. The vessel is filled with dilute gas containing two types of molecule which differ because they contain different atomic
isotopes, and thus have the different masses,
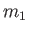 and
and 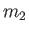 . The concentrations of these molecules are
. The concentrations of these molecules are
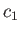 and
and 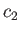 , respectively, and are maintained constant within the vessel by constantly replenishing the supply of gas
in it.
, respectively, and are maintained constant within the vessel by constantly replenishing the supply of gas
in it.
- Let
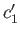 and
and 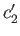 be the concentrations of the two types of molecule in the collecting chamber. What is the ratio
be the concentrations of the two types of molecule in the collecting chamber. What is the ratio
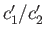 ?
?
- By using the gas
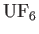 , one can attempt to separate
, one can attempt to separate
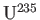 from
from
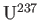 , the first of
these isotopes being the one that undergoes nuclear fission reactions. The molecules in the vessel are then
, the first of
these isotopes being the one that undergoes nuclear fission reactions. The molecules in the vessel are then
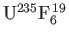 and
and
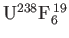 . The concentrations of these molecules in the vessel
corresponds to the natural abundances of the two isotopes:
. The concentrations of these molecules in the vessel
corresponds to the natural abundances of the two isotopes:
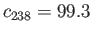 percent, and
percent, and
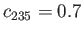 percent. What is the
ratio,
percent. What is the
ratio,
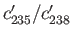 , of the two isotopic concentrations in the gas collected after effusion, compared to the
original concentration ratio,
, of the two isotopic concentrations in the gas collected after effusion, compared to the
original concentration ratio,
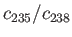 ?
?
- Show that the mean force per unit area exerted on the walls of a container enclosing a Maxwellian gas is
where 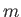 is the molecular mass, and the outward normal to the wall element is directed in the
is the molecular mass, and the outward normal to the wall element is directed in the 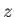 -direction. Hence, deduce that
-direction. Hence, deduce that
where 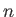 is the molecular concentration, and
is the molecular concentration, and  the absolute gas temperature.
the absolute gas temperature.
- Consider a spin-1/2 ferromagnetic material consisting of
 identical atoms with
identical atoms with 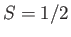 and
and 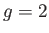 . Let each atom have
. Let each atom have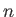 nearest neighbors.
nearest neighbors.
- Show that
where
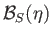 is a Brillouin function.
is a Brillouin function.
- Use the molecular field approximation to demonstrate that
where
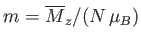 ,
,
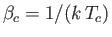 , and
, and
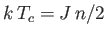 .
.
- Show that for
 slightly less than
slightly less than 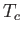 , and in the absence of an external magnetic field,
, and in the absence of an external magnetic field,
- Demonstrate that exactly at the critical temperature,
- Finally, show that for
 slightly larger than
slightly larger than 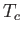 ,
,
[Hint: At small arguments
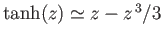 .]
.]



Next: Quantum Statistics
Up: Applications of Statistical Thermodynamics
Previous: Ferromagnetism
Richard Fitzpatrick
2016-01-25
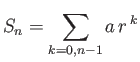
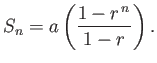
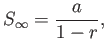
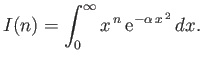
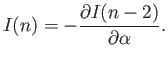
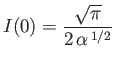
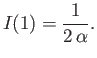
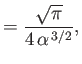
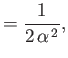
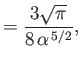
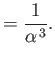
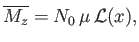
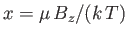 , and
, and
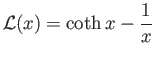
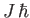 is
is
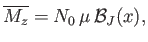
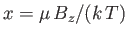 ,
,
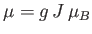 ,
and
,
and
![$\displaystyle {\cal B}_J(x)=
\left[\left(\frac{2 J+1}{2 J}\right)\coth\left(\...
... J+1}{2 J} x\right)-\frac{1}{2 J} \coth\left(\frac{x}{2 J}\right)\right]
$](img1876.png)
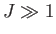 . (This is the classical
limit because the spacing between adjacent magnetic energy levels,
. (This is the classical
limit because the spacing between adjacent magnetic energy levels,
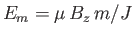 , where
, where 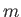 is an integer lying between
is an integer lying between 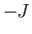 and
and 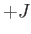 , is
, is
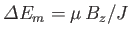 , which tends to zero as
, which tends to zero as
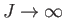 .)
.)
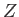 , is such that
, is such that
![$\displaystyle \ln Z = N \ln\left[2 \cosh\left(\frac{\mu_B B_z}{k T}\right)\right],
$](img1881.png)
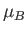 is the Bohr magneton,
is the Bohr magneton, 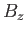 the magnetic field-strength, and
the magnetic field-strength, and  the absolute temperature.
the absolute temperature.
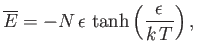
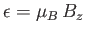 .
Show that
.
Show that
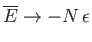 as
as
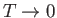 , and
, and
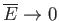 as
as
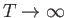 .
Plot
.
Plot
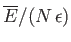 versus
versus
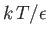 .
.
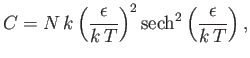
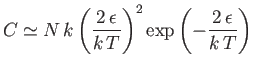
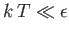 , whereas
, whereas
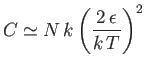
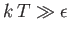 . Plot
. Plot 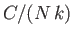 versus
versus
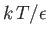 . The sharp peak that is evident when
. The sharp peak that is evident when
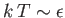 is
known as the Schottky anomaly.
is
known as the Schottky anomaly.
 as
as
 and
and
 as
as
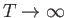 .
Plot
.
Plot 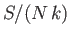 versus
versus
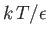 .
.
 , of the nuclear
contribution to the molar internal energy of the solid.
, of the nuclear
contribution to the molar internal energy of the solid.
 , of the nuclear contribution to
the molar entropy of the solid.
, of the nuclear contribution to
the molar entropy of the solid.
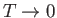 and
and
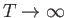 .
.
 ?
?
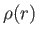 , of molecules varies with their radial
distance,
, of molecules varies with their radial
distance, 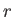 , from the axis of rotation.
, from the axis of rotation.
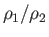 at the radii
at the radii 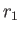 and
and 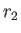 is measured by optical means.
is measured by optical means.
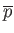 .
.
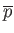 , of the gas related to the so-called
partial pressure,
, of the gas related to the so-called
partial pressure,
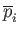 , that the
, that the 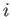 th gas would produce if it alone
occupied the entire volume at this temperature?
th gas would produce if it alone
occupied the entire volume at this temperature?
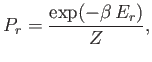
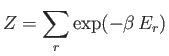
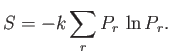
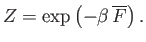
![$\displaystyle \ln Z = N\left[\ln\left(\frac{V}{N}\right)-\frac{3}{2} \ln\beta +\sigma\right],
$](img1919.png)
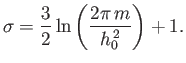
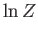
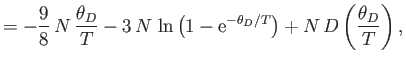
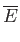
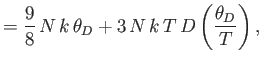
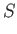
![$\displaystyle = N k\left[-3 \ln\left(1-{\rm e}^{-\theta_D/T}\right)+4 D\left(\frac{\theta_D}{T}\right)\right].$](img1932.png)
 is the number of atoms in the solid,
is the number of atoms in the solid,  the absolute temperature,
the absolute temperature, 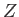 the partition function,
the partition function,
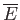 the mean energy,
the mean energy, 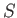 the
entropy,
the
entropy,
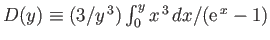 ,
,
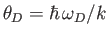 , and
, and 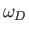 is the Debye frequency.
is the Debye frequency.
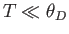 ,
,
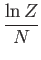
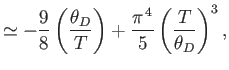
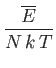
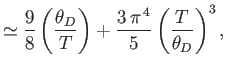
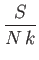
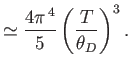
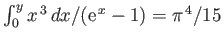 .]
.]
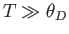 ,
,
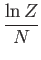
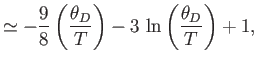
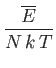
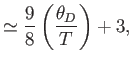
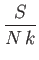
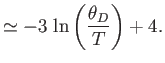
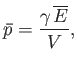
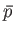 is the mean pressure,
is the mean pressure,  the volume, and
the volume, and
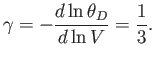
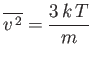
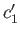 and
and 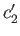 be the concentrations of the two types of molecule in the collecting chamber. What is the ratio
be the concentrations of the two types of molecule in the collecting chamber. What is the ratio
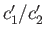 ?
?
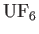 , one can attempt to separate
, one can attempt to separate
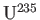 from
from
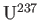 , the first of
these isotopes being the one that undergoes nuclear fission reactions. The molecules in the vessel are then
, the first of
these isotopes being the one that undergoes nuclear fission reactions. The molecules in the vessel are then
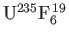 and
and
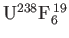 . The concentrations of these molecules in the vessel
corresponds to the natural abundances of the two isotopes:
. The concentrations of these molecules in the vessel
corresponds to the natural abundances of the two isotopes:
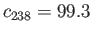 percent, and
percent, and
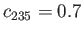 percent. What is the
ratio,
percent. What is the
ratio,
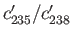 , of the two isotopic concentrations in the gas collected after effusion, compared to the
original concentration ratio,
, of the two isotopic concentrations in the gas collected after effusion, compared to the
original concentration ratio,
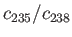 ?
?
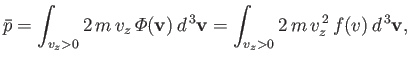
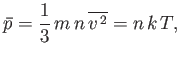
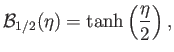
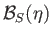 is a Brillouin function.
is a Brillouin function.
![$\displaystyle m = \tanh\left[\frac{\beta}{\beta_c}\left(m+\beta_c \mu_B B_z\right)\right],$](img1972.png)
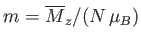 ,
,
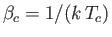 , and
, and
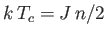 .
.
 slightly less than
slightly less than 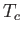 , and in the absence of an external magnetic field,
, and in the absence of an external magnetic field,
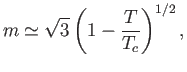
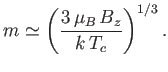
 slightly larger than
slightly larger than 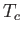 ,
,
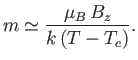
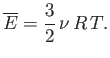
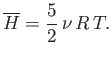
![$\displaystyle \overline{F} = -\nu R T\left[\ln\left(\frac{V}{N}\right)-\frac{3}{2} \ln\beta +\sigma\right].
$](img1924.png)
![$\displaystyle \overline{G} = -\nu R T\left[\ln\left(\frac{V}{N}\right)-\frac{3}{2} \ln\beta +\sigma-1\right].
$](img1925.png)