


Next: Statistical Thermodynamics
Up: Heat and Work
Previous: Exact and Inexact Differentials
- The mean pressure,
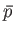 , of a thermally insulated gas varies
with volume according to the relation
, of a thermally insulated gas varies
with volume according to the relation
where 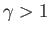 and
and 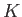 are positive constants. Show that the work done
by this gas in a quasi-static process in which the state of the gas
evolves from an initial macrostate with pressure
are positive constants. Show that the work done
by this gas in a quasi-static process in which the state of the gas
evolves from an initial macrostate with pressure 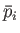 and
volume
and
volume 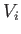 to a final macrostate with pressure
to a final macrostate with pressure 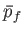 and
volume
and
volume 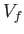 is
is
- Consider the infinitesimal quantity
Is this an exact differential? If not, find the integrating factor that converts it into an exact differential.
- A system undergoes a quasi-static process that appears as a closed curve in a diagram of mean pressure,
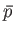 , versus volume,
, versus volume,  .
Such a process is termed cyclic, because the system ends up in a final macrostate that is identical to its initial macrostate.
Show that the work done by the system is given by the area contained within the closed curve in the
.
Such a process is termed cyclic, because the system ends up in a final macrostate that is identical to its initial macrostate.
Show that the work done by the system is given by the area contained within the closed curve in the 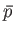 -
- plane.
plane.



Next: Statistical Thermodynamics
Up: Heat and Work
Previous: Exact and Inexact Differentials
Richard Fitzpatrick
2016-01-25

