


Next: Exercises
Up: Central Potentials
Previous: Hydrogen Atom
An electron in a given stationary state of a hydrogen atom, characterized
by the quantum numbers 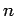 ,
, 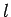 , and
, and 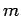 , should, in principle,
remain in that state indefinitely. In practice, if the state is slightly
perturbed--e.g., by interacting with a photon--then the electron can make a transition to another stationary
state with different quantum numbers.
, should, in principle,
remain in that state indefinitely. In practice, if the state is slightly
perturbed--e.g., by interacting with a photon--then the electron can make a transition to another stationary
state with different quantum numbers.
Suppose that an electron in a hydrogen atom
makes a transition from an initial state whose radial quantum
number is  to a final state whose radial quantum number is
to a final state whose radial quantum number is 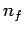 .
According to Eq. (676), the energy of the electron
will change by
.
According to Eq. (676), the energy of the electron
will change by
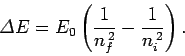 |
(699) |
If
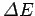 is negative then we would expect the electron
to emit a photon of frequency
is negative then we would expect the electron
to emit a photon of frequency
 [see Eq. (58)]. Likewise, if
[see Eq. (58)]. Likewise, if
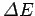 is positive then the electron
must absorb a photon of energy
is positive then the electron
must absorb a photon of energy
 .
Given that
.
Given that
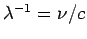 , the possible wavelengths of
the photons emitted by a hydrogen atom as its electron makes
transitions between different energy levels are
, the possible wavelengths of
the photons emitted by a hydrogen atom as its electron makes
transitions between different energy levels are
 |
(700) |
where
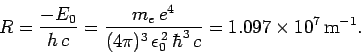 |
(701) |
Here, it is assumed that 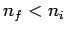 . Note that the emission spectrum
of hydrogen is quantized: i.e., a hydrogen atom
can only emit photons with certain fixed set of wavelengths. Likewise, a hydrogen
atom can only absorb photons which have the same fixed set of wavelengths.
This set of wavelengths constitutes the characteristic emission/absorption
spectrum of the hydrogen atom, and can be observed as ``spectral lines'' using a spectroscope.
. Note that the emission spectrum
of hydrogen is quantized: i.e., a hydrogen atom
can only emit photons with certain fixed set of wavelengths. Likewise, a hydrogen
atom can only absorb photons which have the same fixed set of wavelengths.
This set of wavelengths constitutes the characteristic emission/absorption
spectrum of the hydrogen atom, and can be observed as ``spectral lines'' using a spectroscope.
Equation (700) is known as the Rydberg formula. Likewise,
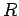 is called the Rydberg constant. The Rydberg formula
was actually discovered empirically in the nineteenth century by spectroscopists, and was first explained theoretically by Bohr in 1913 using a primitive version of quantum mechanics. Transitions to the ground-state (
is called the Rydberg constant. The Rydberg formula
was actually discovered empirically in the nineteenth century by spectroscopists, and was first explained theoretically by Bohr in 1913 using a primitive version of quantum mechanics. Transitions to the ground-state (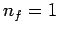 ) give rise to spectral lines in the ultraviolet band--this set of
lines is called the Lyman series. Transitions to the first excited
state (
) give rise to spectral lines in the ultraviolet band--this set of
lines is called the Lyman series. Transitions to the first excited
state (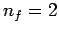 ) give rise to spectral lines in the visible band--this
set of lines is called the Balmer series. Transitions to the second excited
state (
) give rise to spectral lines in the visible band--this
set of lines is called the Balmer series. Transitions to the second excited
state (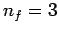 ) give rise to spectral lines in the infrared band--this
set of lines is called the Paschen series, and so on.
) give rise to spectral lines in the infrared band--this
set of lines is called the Paschen series, and so on.
Subsections



Next: Exercises
Up: Central Potentials
Previous: Hydrogen Atom
Richard Fitzpatrick
2010-07-20
![]() to a final state whose radial quantum number is
to a final state whose radial quantum number is ![]() .
According to Eq. (676), the energy of the electron
will change by
.
According to Eq. (676), the energy of the electron
will change by
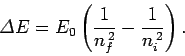
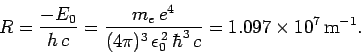
![]() is called the Rydberg constant. The Rydberg formula
was actually discovered empirically in the nineteenth century by spectroscopists, and was first explained theoretically by Bohr in 1913 using a primitive version of quantum mechanics. Transitions to the ground-state (
is called the Rydberg constant. The Rydberg formula
was actually discovered empirically in the nineteenth century by spectroscopists, and was first explained theoretically by Bohr in 1913 using a primitive version of quantum mechanics. Transitions to the ground-state (![]() ) give rise to spectral lines in the ultraviolet band--this set of
lines is called the Lyman series. Transitions to the first excited
state (
) give rise to spectral lines in the ultraviolet band--this set of
lines is called the Lyman series. Transitions to the first excited
state (![]() ) give rise to spectral lines in the visible band--this
set of lines is called the Balmer series. Transitions to the second excited
state (
) give rise to spectral lines in the visible band--this
set of lines is called the Balmer series. Transitions to the second excited
state (![]() ) give rise to spectral lines in the infrared band--this
set of lines is called the Paschen series, and so on.
) give rise to spectral lines in the infrared band--this
set of lines is called the Paschen series, and so on.