


Next: Hydrogen Atom
Up: Central Potentials
Previous: Derivation of Radial Equation
Infinite Spherical Potential Well
Consider a particle of mass 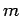 and energy
and energy 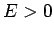 moving in the
following simple central potential:
moving in the
following simple central potential:
![\begin{displaymath}
V(r) = \left\{\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&\mbox...
...leq a$}\ [0.5ex]
\infty&&\mbox{otherwise}
\end{array}\right..
\end{displaymath}](img1537.png) |
(647) |
Clearly, the wavefunction 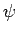 is only non-zero in the region
is only non-zero in the region
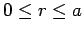 .
Within this region, it is subject to the physical boundary conditions that it be well behaved (i.e.,
square-integrable) at
.
Within this region, it is subject to the physical boundary conditions that it be well behaved (i.e.,
square-integrable) at 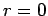 , and that it be zero at
, and that it be zero at 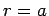 (see Sect. 5.2).
Writing the wavefunction in the standard form
(see Sect. 5.2).
Writing the wavefunction in the standard form
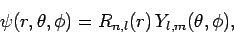 |
(648) |
we deduce (see previous section) that the radial function 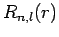 satisfies
satisfies
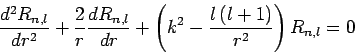 |
(649) |
in the region
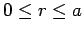 , where
, where
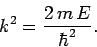 |
(650) |
Figure 20:
The first few spherical Bessel functions. The solid, short-dashed, long-dashed, and dot-dashed curves show  ,
, 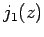 ,
, 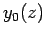 , and
, and 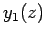 , respectively.
, respectively.
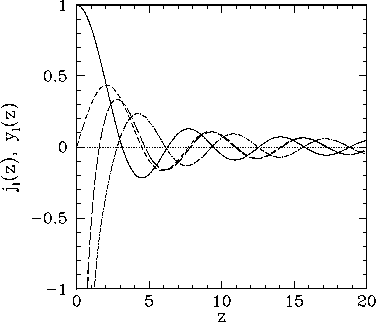 |
Defining the scaled radial variable 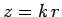 , the above differential
equation can be transformed into the standard form
, the above differential
equation can be transformed into the standard form
![\begin{displaymath}
\frac{d^2 R_{n,l}}{dz^2} + \frac{2}{z}\frac{dR_{n,l}}{dz} + \left[1
- \frac{l (l+1)}{z^2}\right] R_{n,l} = 0.
\end{displaymath}](img1546.png) |
(651) |
The two independent solutions to this well-known second-order differential equation are called spherical Bessel
functions,![[*]](footnote.png) and can be written
and can be written
Thus, the first few spherical Bessel functions take the form
These functions are also plotted in Fig. 20. It can be seen that
the spherical Bessel functions are oscillatory in nature, passing through
zero many times. However, the 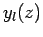 functions are badly
behaved (i.e., they are not square-integrable) at
functions are badly
behaved (i.e., they are not square-integrable) at 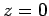 , whereas
the
, whereas
the 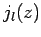 functions are well behaved everywhere. It follows from
our boundary condition at
functions are well behaved everywhere. It follows from
our boundary condition at 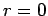 that the
that the 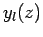 are unphysical, and that the radial wavefunction
are unphysical, and that the radial wavefunction 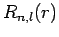 is thus proportional to
is thus proportional to 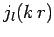 only. In order to satisfy the boundary
condition at
only. In order to satisfy the boundary
condition at 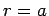 [i.e.,
[i.e., 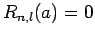 ], the value of
], the value of 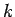 must
be chosen such that
must
be chosen such that 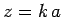 corresponds to one of the zeros of
corresponds to one of the zeros of 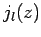 .
Let us denote the
.
Let us denote the 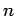 th zero of
th zero of 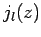 as
as 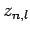 . It follows that
. It follows that
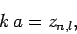 |
(658) |
for
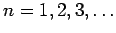 .
Hence, from (650), the allowed energy levels are
.
Hence, from (650), the allowed energy levels are
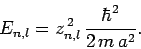 |
(659) |
The first few values of 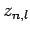 are listed in Table 1. It
can be seen that
are listed in Table 1. It
can be seen that 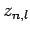 is an increasing function of both
is an increasing function of both 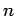 and
and 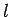 .
.
Table 1:
The first few zeros of the spherical Bessel function 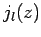 .
.
| |
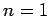 |
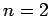 |
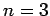 |
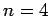 |
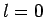 |
3.142 |
6.283 |
9.425 |
12.566 |
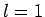 |
4.493 |
7.725 |
10.904 |
14.066 |
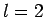 |
5.763 |
9.095 |
12.323 |
15.515 |
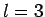 |
6.988 |
10.417 |
13.698 |
16.924 |
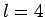 |
8.183 |
11.705 |
15.040 |
18.301 |
|
We are now in a position to interpret the three quantum numbers--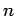 ,
, 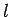 ,
and
,
and 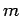 --which determine the form of the wavefunction
specified in Eq. (648). As is clear from Sect. 8, the
azimuthal quantum number
--which determine the form of the wavefunction
specified in Eq. (648). As is clear from Sect. 8, the
azimuthal quantum number 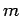 determines the number of nodes in the
wavefunction as the azimuthal angle
determines the number of nodes in the
wavefunction as the azimuthal angle 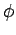 varies between 0 and
varies between 0 and 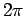 . Thus,
. Thus, 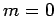 corresponds to no nodes,
corresponds to no nodes, 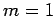 to a single node,
to a single node, 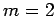 to two nodes,
etc. Likewise, the polar quantum number
to two nodes,
etc. Likewise, the polar quantum number 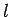 determines the
number of nodes in the wavefunction as the polar angle
determines the
number of nodes in the wavefunction as the polar angle 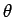 varies between 0 and
varies between 0 and 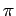 .
Again,
.
Again, 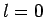 corresponds to no nodes,
corresponds to no nodes, 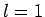 to a single node,
etc. Finally, the radial quantum number
to a single node,
etc. Finally, the radial quantum number 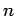 determines
the number of nodes in the wavefunction as the radial
variable
determines
the number of nodes in the wavefunction as the radial
variable 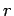 varies between 0 and
varies between 0 and 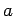 (not counting any
nodes at
(not counting any
nodes at 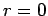 or
or 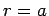 ). Thus,
). Thus, 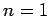 corresponds to no nodes,
corresponds to no nodes,
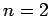 to a single node,
to a single node, 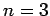 to two nodes, etc. Note that,
for the
case of an infinite potential well,
the only restrictions on the values that the various quantum numbers can take are that
to two nodes, etc. Note that,
for the
case of an infinite potential well,
the only restrictions on the values that the various quantum numbers can take are that 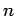 must be a positive integer,
must be a positive integer, 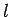 must be
a non-negative integer, and
must be
a non-negative integer, and 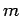 must be an integer lying between
must be an integer lying between 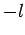 and
and 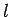 . Note, further,
that the allowed energy levels (659) only depend on the
values of the quantum numbers
. Note, further,
that the allowed energy levels (659) only depend on the
values of the quantum numbers 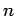 and
and 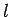 . Finally, it is
easily demonstrated that the spherical Bessel functions are mutually
orthogonal: i.e.,
. Finally, it is
easily demonstrated that the spherical Bessel functions are mutually
orthogonal: i.e.,
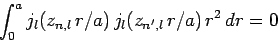 |
(660) |
when 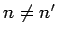 .
Given that the
.
Given that the
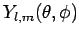 are mutually orthogonal (see Sect. 8), this ensures that wavefunctions (648) corresponding to distinct
sets of values of the quantum numbers
are mutually orthogonal (see Sect. 8), this ensures that wavefunctions (648) corresponding to distinct
sets of values of the quantum numbers 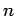 ,
, 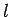 , and
, and 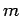 are mutually
orthogonal.
are mutually
orthogonal.



Next: Hydrogen Atom
Up: Central Potentials
Previous: Derivation of Radial Equation
Richard Fitzpatrick
2010-07-20
![\begin{displaymath}
V(r) = \left\{\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&\mbox...
...leq a$}\ [0.5ex]
\infty&&\mbox{otherwise}
\end{array}\right..
\end{displaymath}](img1537.png)
![\begin{displaymath}
V(r) = \left\{\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&\mbox...
...leq a$}\ [0.5ex]
\infty&&\mbox{otherwise}
\end{array}\right..
\end{displaymath}](img1537.png)

![]() , the above differential
equation can be transformed into the standard form
, the above differential
equation can be transformed into the standard form
![\begin{displaymath}
\frac{d^2 R_{n,l}}{dz^2} + \frac{2}{z}\frac{dR_{n,l}}{dz} + \left[1
- \frac{l (l+1)}{z^2}\right] R_{n,l} = 0.
\end{displaymath}](img1546.png)
![[*]](footnote.png) and can be written
and can be written
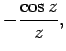
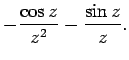
![]() ,
, ![]() ,
and
,
and ![]() --which determine the form of the wavefunction
specified in Eq. (648). As is clear from Sect. 8, the
azimuthal quantum number
--which determine the form of the wavefunction
specified in Eq. (648). As is clear from Sect. 8, the
azimuthal quantum number ![]() determines the number of nodes in the
wavefunction as the azimuthal angle
determines the number of nodes in the
wavefunction as the azimuthal angle ![]() varies between 0 and
varies between 0 and ![]() . Thus,
. Thus, ![]() corresponds to no nodes,
corresponds to no nodes, ![]() to a single node,
to a single node, ![]() to two nodes,
etc. Likewise, the polar quantum number
to two nodes,
etc. Likewise, the polar quantum number ![]() determines the
number of nodes in the wavefunction as the polar angle
determines the
number of nodes in the wavefunction as the polar angle ![]() varies between 0 and
varies between 0 and ![]() .
Again,
.
Again, ![]() corresponds to no nodes,
corresponds to no nodes, ![]() to a single node,
etc. Finally, the radial quantum number
to a single node,
etc. Finally, the radial quantum number ![]() determines
the number of nodes in the wavefunction as the radial
variable
determines
the number of nodes in the wavefunction as the radial
variable ![]() varies between 0 and
varies between 0 and ![]() (not counting any
nodes at
(not counting any
nodes at ![]() or
or ![]() ). Thus,
). Thus, ![]() corresponds to no nodes,
corresponds to no nodes,
![]() to a single node,
to a single node, ![]() to two nodes, etc. Note that,
for the
case of an infinite potential well,
the only restrictions on the values that the various quantum numbers can take are that
to two nodes, etc. Note that,
for the
case of an infinite potential well,
the only restrictions on the values that the various quantum numbers can take are that ![]() must be a positive integer,
must be a positive integer, ![]() must be
a non-negative integer, and
must be
a non-negative integer, and ![]() must be an integer lying between
must be an integer lying between ![]() and
and ![]() . Note, further,
that the allowed energy levels (659) only depend on the
values of the quantum numbers
. Note, further,
that the allowed energy levels (659) only depend on the
values of the quantum numbers ![]() and
and ![]() . Finally, it is
easily demonstrated that the spherical Bessel functions are mutually
orthogonal: i.e.,
. Finally, it is
easily demonstrated that the spherical Bessel functions are mutually
orthogonal: i.e.,