


Next: Eigenvalues of
Up: Orbital Angular Momentum
Previous: Representation of Angular Momentum
Eigenstates of Angular Momentum
Let us find the simultaneous eigenstates of the angular momentum
operators 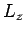 and
and 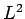 . Since both of these operators can
be represented as purely angular differential operators, it stands to
reason that their eigenstates only depend on the angular coordinates
. Since both of these operators can
be represented as purely angular differential operators, it stands to
reason that their eigenstates only depend on the angular coordinates
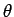 and
and 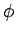 . Thus,
we can write
. Thus,
we can write
Here, the
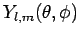 are the eigenstates in question, whereas the dimensionless
quantities
are the eigenstates in question, whereas the dimensionless
quantities  and
and 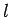 parameterize the eigenvalues of
parameterize the eigenvalues of 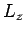 and
and 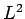 ,
which are
,
which are 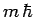 and
and
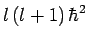 , respectively. Of course,
we expect the
, respectively. Of course,
we expect the 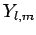 to be both mutually orthogonal and properly normalized
(see Sect. 4.9), so that
to be both mutually orthogonal and properly normalized
(see Sect. 4.9), so that
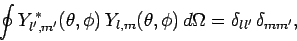 |
(558) |
where
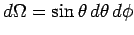 is an element of solid angle,
and the integral is over all solid angle.
is an element of solid angle,
and the integral is over all solid angle.
Now,
where use has been made of Eq. (543). We, thus, conclude that
when the operator  operates on an eigenstate of
operates on an eigenstate of 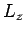 corresponding to the eigenvalue
corresponding to the eigenvalue 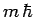 it converts it to an
eigenstate corresponding to the eigenvalue
it converts it to an
eigenstate corresponding to the eigenvalue 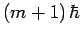 .
Hence,
.
Hence,  is known as the raising operator (for
is known as the raising operator (for 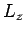 ). It is
also easily demonstrated that
). It is
also easily demonstrated that
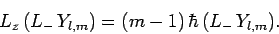 |
(560) |
In other words, when 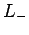 operates on an eigenstate of
operates on an eigenstate of 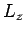 corresponding to the eigenvalue
corresponding to the eigenvalue 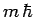 it converts it to an
eigenstate corresponding to the eigenvalue
it converts it to an
eigenstate corresponding to the eigenvalue 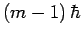 .
Hence,
.
Hence, 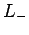 is known as the lowering operator (for
is known as the lowering operator (for 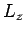 ).
).
Writing
we obtain
![\begin{displaymath}
L_- L_+ Y_{l,m} = c^+_{l,m} c^-_{l,m+1} Y_{l,m} =
[l (l+1)-m (m+1)] \hbar^2 Y_{l,m},
\end{displaymath}](img1382.png) |
(563) |
where use has been made of Eq. (541). Likewise,
![\begin{displaymath}
L_+ L_- Y_{l,m} = c^+_{l,m-1} c^-_{l,m} Y_{l,m} = [l (l+1)-m (m-1)] \hbar^2 Y_{l,m},
\end{displaymath}](img1383.png) |
(564) |
where use has been made of Eq. (540). It
follows that
These equations are satisfied when
![\begin{displaymath}
c^\pm_{l,m} = [l (l+l) - m (m\pm 1)]^{1/2} \hbar.
\end{displaymath}](img1388.png) |
(567) |
Hence, we can write



Next: Eigenvalues of
Up: Orbital Angular Momentum
Previous: Representation of Angular Momentum
Richard Fitzpatrick
2010-07-20