


Next: Eigenstates of Angular Momentum
Up: Orbital Angular Momentum
Previous: Angular Momentum Operators
Representation of Angular Momentum
Now, we saw earlier, in Sect. 7.2, that the operators, 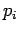 , which represent
the Cartesian components of linear momentum in quantum mechanics, can be represented
as the spatial differential operators
, which represent
the Cartesian components of linear momentum in quantum mechanics, can be represented
as the spatial differential operators
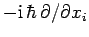 .
Let us now investigate whether angular momentum operators can similarly
be represented as spatial differential operators.
.
Let us now investigate whether angular momentum operators can similarly
be represented as spatial differential operators.
It is most convenient to perform our investigation using conventional
spherical polar coordinates: i.e., 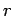 ,
, 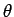 , and
, and 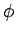 . These are
defined with respect to our usual Cartesian coordinates as follows:
. These are
defined with respect to our usual Cartesian coordinates as follows:
It follows, after some tedious analysis, that
Making use of the definitions (527)-(529), (534), and (538), the fundamental representation (478)-(480) of the 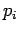 operators as spatial differential operators, the Eqs. (545)-(550), and a great deal of tedious algebra, we finally obtain
operators as spatial differential operators, the Eqs. (545)-(550), and a great deal of tedious algebra, we finally obtain
as well as
![\begin{displaymath}
L^2 = -\hbar^2\left[\frac{1}{\sin\theta}\frac{\partial}{\par...
...frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right],
\end{displaymath}](img1360.png) |
(554) |
and
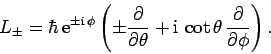 |
(555) |
We, thus, conclude that all of our angular momentum operators can be represented
as differential operators involving the angular spherical
coordinates, 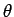 and
and 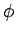 , but not involving the radial coordinate,
, but not involving the radial coordinate,
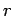 .
.



Next: Eigenstates of Angular Momentum
Up: Orbital Angular Momentum
Previous: Angular Momentum Operators
Richard Fitzpatrick
2010-07-20
![]() ,
, ![]() , and
, and ![]() . These are
defined with respect to our usual Cartesian coordinates as follows:
. These are
defined with respect to our usual Cartesian coordinates as follows:
![\begin{displaymath}
L^2 = -\hbar^2\left[\frac{1}{\sin\theta}\frac{\partial}{\par...
...frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right],
\end{displaymath}](img1360.png)