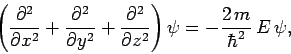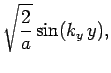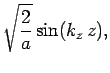Next: Degenerate Electron Gases
Up: Three-Dimensional Quantum Mechanics
Previous: Fundamental Concepts
Consider a particle of mass  trapped inside a cubic box of dimension
trapped inside a cubic box of dimension 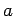 (see Sect. 5.2). The particle's stationary wavefunction,
(see Sect. 5.2). The particle's stationary wavefunction, 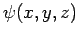 , satisfies
, satisfies
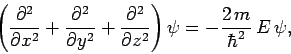 |
(492) |
where 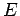 is the particle energy. The wavefunction satisfies the boundary
condition that it must be zero at the edges of the box.
is the particle energy. The wavefunction satisfies the boundary
condition that it must be zero at the edges of the box.
Let us search for a separable solution to the above equation of the
form
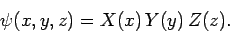 |
(493) |
The factors of the wavefunction satisfy the boundary conditions
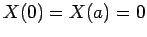 ,
, 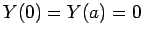 , and
, and 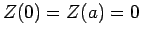 .
Substituting (493) into Eq. (492), and rearranging, we
obtain
.
Substituting (493) into Eq. (492), and rearranging, we
obtain
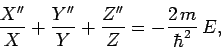 |
(494) |
where 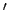 denotes a derivative with respect to argument. It is evident that
the only way in which the above equation can be satisfied at all points
within the box is if
denotes a derivative with respect to argument. It is evident that
the only way in which the above equation can be satisfied at all points
within the box is if
where 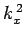 ,
, 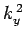 , and
, and 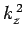 are spatial constants. Note that the right-hand
sides of the above equations must contain negative, rather than positive,
spatial constants, because it would not otherwise be possible to satisfy the
boundary conditions. The solutions to the above equations which are properly
normalized, and satisfy the boundary conditions, are [see Eq. (310)]
are spatial constants. Note that the right-hand
sides of the above equations must contain negative, rather than positive,
spatial constants, because it would not otherwise be possible to satisfy the
boundary conditions. The solutions to the above equations which are properly
normalized, and satisfy the boundary conditions, are [see Eq. (310)]
where
Here,  ,
, 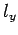 , and
, and 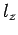 are positive integers.
Thus, from Eqs. (494)-(497), the energy is written [see Eq. (308)]
are positive integers.
Thus, from Eqs. (494)-(497), the energy is written [see Eq. (308)]
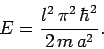 |
(504) |
where
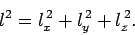 |
(505) |



Next: Degenerate Electron Gases
Up: Three-Dimensional Quantum Mechanics
Previous: Fundamental Concepts
Richard Fitzpatrick
2010-07-20