


Next: Infinite Potential Well
Up: One-Dimensional Potentials
Previous: One-Dimensional Potentials
In this chapter, we shall investigate the interaction of
a non-relativistic particle of mass  and energy
and energy 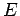 with various
one-dimensional potentials,
with various
one-dimensional potentials, 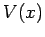 . Since we are searching for stationary
solutions with unique energies, we can write the wavefunction in the form (see Sect. 4.12)
. Since we are searching for stationary
solutions with unique energies, we can write the wavefunction in the form (see Sect. 4.12)
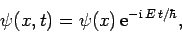 |
(300) |
where 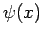 satisfies the time-independent Schrödinger equation:
satisfies the time-independent Schrödinger equation:
![\begin{displaymath}
\frac{d^2 \psi}{d x^2} = \frac{2 m}{\hbar^2}
\left[V(x)-E\right]\psi.
\end{displaymath}](img787.png) |
(301) |
In general, the solution, 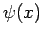 , to the above equation must be
finite, otherwise the probability density
, to the above equation must be
finite, otherwise the probability density 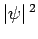 would
become infinite (which is unphysical). Likewise, the solution must be
continuous, otherwise the
probability current (155) would become infinite (which is also
unphysical).
would
become infinite (which is unphysical). Likewise, the solution must be
continuous, otherwise the
probability current (155) would become infinite (which is also
unphysical).
Richard Fitzpatrick
2010-07-20