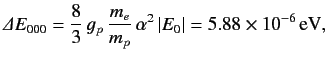Next: Exercises
Up: Time-Independent Perturbation Theory
Previous: Zeeman Effect
The proton in a hydrogen atom is a spin one-half charged particle, and therefore
possesses a magnetic moment. By analogy with Equation (681),
we can write
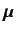 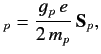 |
(726) |
where
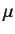
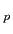 is the proton magnetic
moment,
is the proton magnetic
moment, 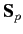 is the proton spin, and the proton gyromagnetic ratio
is the proton spin, and the proton gyromagnetic ratio 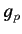 is found experimentally to take that value
is found experimentally to take that value 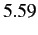 . Note that the
magnetic moment of a proton is much smaller (by a factor of order
. Note that the
magnetic moment of a proton is much smaller (by a factor of order 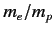 )
than that of an electron.
According
to classical electromagnetism, the proton's magnetic moment generates a
magnetic field of the form
)
than that of an electron.
According
to classical electromagnetism, the proton's magnetic moment generates a
magnetic field of the form
![$\displaystyle {\bf B} = \frac{\mu_0}{4\pi\,r^3}\,\left[3\,(\mbox{\boldmath$\mu$...
...$\mu$}_p\right] + \frac{2\,\mu_0}{3}\,\mbox{\boldmath$\mu$}_p\,\delta({\bf x}),$](img1735.png) |
(727) |
where
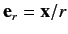 , and
, and
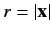 . We can understand the origin of the delta-function term
in the above expression by thinking of the proton as a tiny current loop centred on the origin.
All magnetic field-lines generated by the loop must pass through the loop.
Hence, if the size of the loop goes to zero then the field will be infinite at the origin, and this contribution is what is reflected by the delta-function term. Now, the Hamiltonian of the electron in the magnetic
field generated by the proton is simply
. We can understand the origin of the delta-function term
in the above expression by thinking of the proton as a tiny current loop centred on the origin.
All magnetic field-lines generated by the loop must pass through the loop.
Hence, if the size of the loop goes to zero then the field will be infinite at the origin, and this contribution is what is reflected by the delta-function term. Now, the Hamiltonian of the electron in the magnetic
field generated by the proton is simply
where
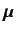 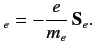 |
(729) |
Here,
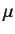
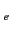 is the electron magnetic moment [see Equation (681)], and
is the electron magnetic moment [see Equation (681)], and 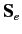 the electron spin. Thus, the
perturbing Hamiltonian is written
the electron spin. Thus, the
perturbing Hamiltonian is written
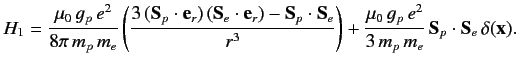 |
(730) |
Note that, because we have neglected coupling between the proton
spin and the magnetic field generated by the electron's orbital motion,
the above expression is only valid for 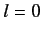 states.
states.
According to standard first-order perturbation theory, the energy-shift induced
by spin-spin coupling between the proton and the electron is the expectation
value of the perturbing Hamiltonian. Hence,
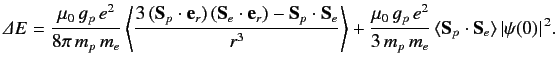 |
(731) |
For the ground-state of hydrogen, which is spherically symmetric,
the first term in the above expression vanishes by symmetry.
Moreover, it is easily demonstrated that
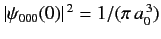 . Thus, we obtain
. Thus, we obtain
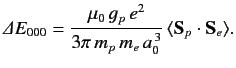 |
(732) |
Let
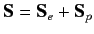 |
(733) |
be the total spin. We can show that
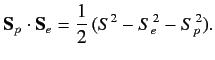 |
(734) |
Thus, the simultaneous eigenstates of the perturbing Hamiltonian
and the main Hamiltonian are the simultaneous eigenstates of 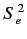 ,
,
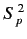 , and
, and 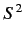 . However, both the proton and
the electron are spin one-half particles. According to Chapter 6,
when two spin one-half particles are combined (in the absence of orbital
angular momentum) the net state has either spin 1 or spin 0.
In fact, there are three spin 1 states, known as triplet states, and a single
spin 0 state, known as the singlet state. For all states,
the eigenvalues of
. However, both the proton and
the electron are spin one-half particles. According to Chapter 6,
when two spin one-half particles are combined (in the absence of orbital
angular momentum) the net state has either spin 1 or spin 0.
In fact, there are three spin 1 states, known as triplet states, and a single
spin 0 state, known as the singlet state. For all states,
the eigenvalues of 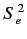 and
and 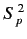 are
are
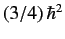 .
The eigenvalue of
.
The eigenvalue of 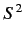 is 0 for the singlet state, and
is 0 for the singlet state, and
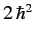 for the triplet states. Hence,
for the triplet states. Hence,
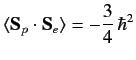 |
(735) |
for the singlet state, and
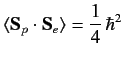 |
(736) |
for the triplet states.
It follows, from the above analysis, that spin-spin coupling breaks
the degeneracy of the two
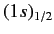 states of the hydrogen atom, lifting the
energy of the triplet configuration, and lowering that of the singlet.
This splitting is known as hyperfine structure.
The net energy difference between the singlet and the triplet states
is
states of the hydrogen atom, lifting the
energy of the triplet configuration, and lowering that of the singlet.
This splitting is known as hyperfine structure.
The net energy difference between the singlet and the triplet states
is
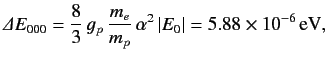 |
(737) |
where
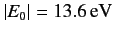 is the (magnitude of the) ground-state energy.
Note that the hyperfine energy-shift is much smaller, by a factor
is the (magnitude of the) ground-state energy.
Note that the hyperfine energy-shift is much smaller, by a factor 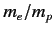 , than
a typical fine structure energy-shift (see Exercise 4).
If we convert the above energy into a wavelength then we obtain
, than
a typical fine structure energy-shift (see Exercise 4).
If we convert the above energy into a wavelength then we obtain
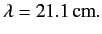 |
(738) |
This is the wavelength of the radiation emitted by a hydrogen atom
that is collisionally excited from the singlet to the triplet
state, and then decays back to the lower energy singlet state.
The 21cm line is famous in radio astronomy because it was used to
map out the spiral structure of our galaxy in the 1950's.



Next: Exercises
Up: Time-Independent Perturbation Theory
Previous: Zeeman Effect
Richard Fitzpatrick
2013-04-08
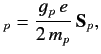
![$\displaystyle {\bf B} = \frac{\mu_0}{4\pi\,r^3}\,\left[3\,(\mbox{\boldmath$\mu$...
...$\mu$}_p\right] + \frac{2\,\mu_0}{3}\,\mbox{\boldmath$\mu$}_p\,\delta({\bf x}),$](img1735.png)
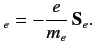
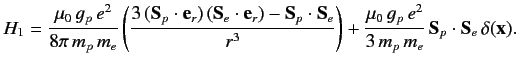
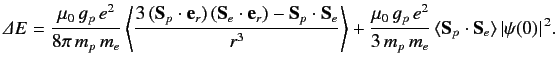
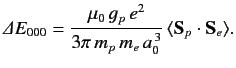
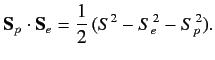
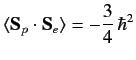
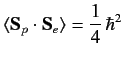
![]() states of the hydrogen atom, lifting the
energy of the triplet configuration, and lowering that of the singlet.
This splitting is known as hyperfine structure.
The net energy difference between the singlet and the triplet states
is
states of the hydrogen atom, lifting the
energy of the triplet configuration, and lowering that of the singlet.
This splitting is known as hyperfine structure.
The net energy difference between the singlet and the triplet states
is