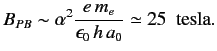Next: Hyperfine Structure
Up: Time-Independent Perturbation Theory
Previous: Fine Structure
Consider a hydrogen-like atom placed in a uniform 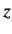 -directed
magnetic field. The change in energy of the outermost electron is
-directed
magnetic field. The change in energy of the outermost electron is
where
 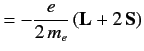 |
(711) |
is its magnetic moment, including both the spin and
orbital contributions.
Thus,
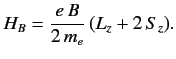 |
(712) |
Suppose that the energy-shifts induced by the magnetic field are much smaller
than those induced by spin-orbit interaction. In this situation,
we can treat 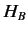 as a small perturbation acting on the
eigenstates of
as a small perturbation acting on the
eigenstates of
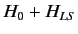 .
Of course, these states are the
simultaneous eigenstates of
.
Of course, these states are the
simultaneous eigenstates of 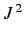 and
and 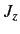 . Let us consider one
of these states, labeled by the quantum numbers
. Let us consider one
of these states, labeled by the quantum numbers 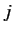 and
and 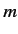 , where
, where
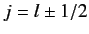 .
From standard perturbation theory, the first-order energy-shift
in the presence of a magnetic field is
.
From standard perturbation theory, the first-order energy-shift
in the presence of a magnetic field is
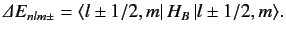 |
(713) |
Because
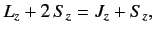 |
(714) |
we find that
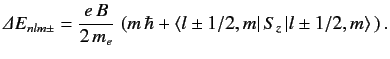 |
(715) |
Now, from Equations (695)-(696),
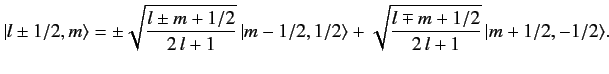 |
(716) |
It follows that
![$\displaystyle \langle l\pm 1/2, m\vert\, S_z\,\vert l\pm 1/2, m\rangle = \frac{...
...+1)} \left[(l\pm m+1/2) - (l\mp m + 1/2) \right] = \pm \frac{m\,\hbar}{2\,l+1}.$](img1700.png) |
(717) |
Thus, we obtain the so-called Lande formula for the energy-shift induced by a
weak magnetic field:
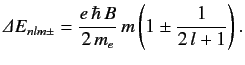 |
(718) |
Let us apply this theory to the sodium atom. We have already seen that
the non-Coulomb potential splits the degeneracy of the 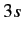 and
and 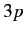 states,
the latter states acquiring a higher energy. The spin-orbit interaction
splits the six
states,
the latter states acquiring a higher energy. The spin-orbit interaction
splits the six 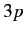 states into two groups, with four
states into two groups, with four 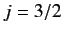 states
lying at a slightly higher energy than two
states
lying at a slightly higher energy than two 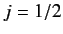 states. According to
Equation (718), a magnetic field splits the
states. According to
Equation (718), a magnetic field splits the
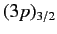 quadruplet of states,
each state acquiring a different energy. In fact, the energy of each state
becomes dependent on the quantum number
quadruplet of states,
each state acquiring a different energy. In fact, the energy of each state
becomes dependent on the quantum number 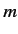 , which measures the
projection of the total angular momentum along the
, which measures the
projection of the total angular momentum along the 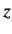 -axis. States with
higher
-axis. States with
higher 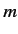 values have higher energies.
A magnetic field also splits the
values have higher energies.
A magnetic field also splits the
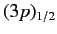 doublet of states. However,
it is evident from Equation (718) that these states are split by a lesser
amount than the
doublet of states. However,
it is evident from Equation (718) that these states are split by a lesser
amount than the 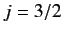 states.
states.
Suppose that we increase the strength of the magnetic
field, so that the energy-shift due to the magnetic field becomes
comparable to the energy-shift induced by spin-orbit interaction.
Clearly, in this situation, it does not make much sense to think
of 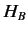 as a small interaction term operating on the eigenstates
of
as a small interaction term operating on the eigenstates
of
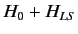 . In fact, this intermediate case is very difficult
to analyze. Let us, instead, consider the extreme limit in which the energy-shift
due to the magnetic field greatly exceeds that induced by spin-orbit effects.
This is called the Paschen-Back limit.
. In fact, this intermediate case is very difficult
to analyze. Let us, instead, consider the extreme limit in which the energy-shift
due to the magnetic field greatly exceeds that induced by spin-orbit effects.
This is called the Paschen-Back limit.
In the Paschen-Back
limit, we can think of the spin-orbit Hamiltonian, 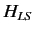 , as
a small interaction term operating on the eigenstates of
, as
a small interaction term operating on the eigenstates of
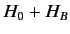 . Note that the magnetic Hamiltonian,
. Note that the magnetic Hamiltonian, 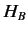 , commutes
with
, commutes
with
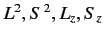 , but does not commute with
, but does not commute with
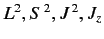 . Thus, in an intense magnetic field, the energy eigenstates of
a hydrogen-like atom are approximate eigenstates of the
spin and orbital angular momenta, but are not eigenstates of the
total angular momentum. We can label each state by the quantum
numbers
. Thus, in an intense magnetic field, the energy eigenstates of
a hydrogen-like atom are approximate eigenstates of the
spin and orbital angular momenta, but are not eigenstates of the
total angular momentum. We can label each state by the quantum
numbers 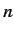 (the energy quantum number),
(the energy quantum number), 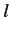 ,
, 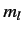 , and
, and 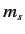 .
Thus, our energy eigenkets are written
.
Thus, our energy eigenkets are written
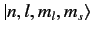 .
The unperturbed Hamiltonian,
.
The unperturbed Hamiltonian, 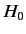 , causes states with different
values of the quantum numbers
, causes states with different
values of the quantum numbers 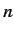 and
and 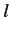 to have different energies.
However, states with the same value of
to have different energies.
However, states with the same value of 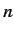 and
and 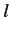 , but different
values of
, but different
values of 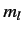 and
and 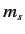 , are degenerate.
The shift in energy due to the magnetic field is simply
, are degenerate.
The shift in energy due to the magnetic field is simply
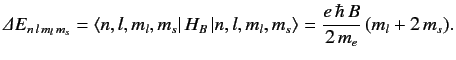 |
(719) |
Thus, states with different values of
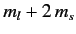 acquire different
energies.
acquire different
energies.
Let us apply this result to a sodium atom. In the absence of
a magnetic field, the six 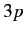 states form two groups of four and
two states, depending on the values of their total angular momentum.
In the presence of an intense magnetic field, the
states form two groups of four and
two states, depending on the values of their total angular momentum.
In the presence of an intense magnetic field, the 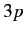 states are split
into five groups. There is a state with
states are split
into five groups. There is a state with
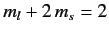 ,
a state with
,
a state with
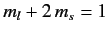 , two states with
, two states with
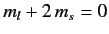 ,
a state with
,
a state with
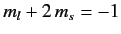 , and a state with
, and a state with
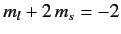 . These groups are equally spaced in energy,
the energy difference between adjacent groups being
. These groups are equally spaced in energy,
the energy difference between adjacent groups being
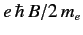 .
.
The energy-shift induced by the spin-orbit Hamiltonian is
given by
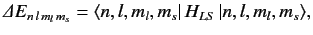 |
(720) |
where
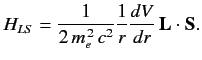 |
(721) |
Now,
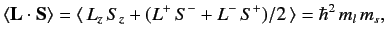 |
(722) |
since
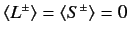 |
(723) |
for expectation values taken between the simultaneous eigenkets of
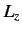 and
and 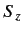 .
Thus,
.
Thus,
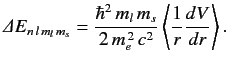 |
(724) |
Let us apply the above result to a sodium atom. In the presence of
an intense magnetic field, the 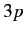 states are split into five
groups with (
states are split into five
groups with (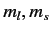 ) quantum numbers
) quantum numbers 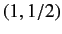 ,
, 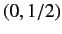 ,
, 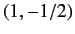 or
or 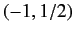 ,
, 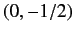 , and
, and 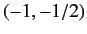 , respectively, in order of
decreasing energy. The spin-orbit term increases the energy of
the highest energy state, does not affect the next highest energy state,
decreases, but does not split, the energy of the doublet, does
not affect the next lowest energy state, and increases
the energy of the lowest
energy state. The net result is that the five groups of states are no
longer equally spaced in energy.
, respectively, in order of
decreasing energy. The spin-orbit term increases the energy of
the highest energy state, does not affect the next highest energy state,
decreases, but does not split, the energy of the doublet, does
not affect the next lowest energy state, and increases
the energy of the lowest
energy state. The net result is that the five groups of states are no
longer equally spaced in energy.
The typical magnetic field-strength needed to access the Paschen-Bach limit
is
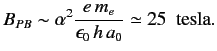 |
(725) |



Next: Hyperfine Structure
Up: Time-Independent Perturbation Theory
Previous: Fine Structure
Richard Fitzpatrick
2013-04-08
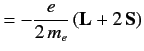
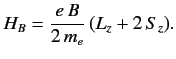
![]() as a small perturbation acting on the
eigenstates of
as a small perturbation acting on the
eigenstates of
![]() .
Of course, these states are the
simultaneous eigenstates of
.
Of course, these states are the
simultaneous eigenstates of ![]() and
and ![]() . Let us consider one
of these states, labeled by the quantum numbers
. Let us consider one
of these states, labeled by the quantum numbers ![]() and
and ![]() , where
, where
![]() .
From standard perturbation theory, the first-order energy-shift
in the presence of a magnetic field is
.
From standard perturbation theory, the first-order energy-shift
in the presence of a magnetic field is
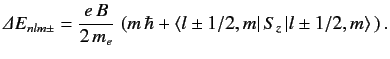
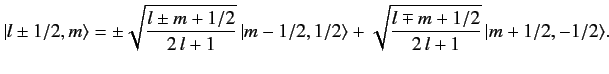
![$\displaystyle \langle l\pm 1/2, m\vert\, S_z\,\vert l\pm 1/2, m\rangle = \frac{...
...+1)} \left[(l\pm m+1/2) - (l\mp m + 1/2) \right] = \pm \frac{m\,\hbar}{2\,l+1}.$](img1700.png)
![]() and
and ![]() states,
the latter states acquiring a higher energy. The spin-orbit interaction
splits the six
states,
the latter states acquiring a higher energy. The spin-orbit interaction
splits the six ![]() states into two groups, with four
states into two groups, with four ![]() states
lying at a slightly higher energy than two
states
lying at a slightly higher energy than two ![]() states. According to
Equation (718), a magnetic field splits the
states. According to
Equation (718), a magnetic field splits the
![]() quadruplet of states,
each state acquiring a different energy. In fact, the energy of each state
becomes dependent on the quantum number
quadruplet of states,
each state acquiring a different energy. In fact, the energy of each state
becomes dependent on the quantum number ![]() , which measures the
projection of the total angular momentum along the
, which measures the
projection of the total angular momentum along the ![]() -axis. States with
higher
-axis. States with
higher ![]() values have higher energies.
A magnetic field also splits the
values have higher energies.
A magnetic field also splits the
![]() doublet of states. However,
it is evident from Equation (718) that these states are split by a lesser
amount than the
doublet of states. However,
it is evident from Equation (718) that these states are split by a lesser
amount than the ![]() states.
states.
![]() as a small interaction term operating on the eigenstates
of
as a small interaction term operating on the eigenstates
of
![]() . In fact, this intermediate case is very difficult
to analyze. Let us, instead, consider the extreme limit in which the energy-shift
due to the magnetic field greatly exceeds that induced by spin-orbit effects.
This is called the Paschen-Back limit.
. In fact, this intermediate case is very difficult
to analyze. Let us, instead, consider the extreme limit in which the energy-shift
due to the magnetic field greatly exceeds that induced by spin-orbit effects.
This is called the Paschen-Back limit.
![]() , as
a small interaction term operating on the eigenstates of
, as
a small interaction term operating on the eigenstates of
![]() . Note that the magnetic Hamiltonian,
. Note that the magnetic Hamiltonian, ![]() , commutes
with
, commutes
with
![]() , but does not commute with
, but does not commute with
![]() . Thus, in an intense magnetic field, the energy eigenstates of
a hydrogen-like atom are approximate eigenstates of the
spin and orbital angular momenta, but are not eigenstates of the
total angular momentum. We can label each state by the quantum
numbers
. Thus, in an intense magnetic field, the energy eigenstates of
a hydrogen-like atom are approximate eigenstates of the
spin and orbital angular momenta, but are not eigenstates of the
total angular momentum. We can label each state by the quantum
numbers ![]() (the energy quantum number),
(the energy quantum number), ![]() ,
, ![]() , and
, and ![]() .
Thus, our energy eigenkets are written
.
Thus, our energy eigenkets are written
![]() .
The unperturbed Hamiltonian,
.
The unperturbed Hamiltonian, ![]() , causes states with different
values of the quantum numbers
, causes states with different
values of the quantum numbers ![]() and
and ![]() to have different energies.
However, states with the same value of
to have different energies.
However, states with the same value of ![]() and
and ![]() , but different
values of
, but different
values of ![]() and
and ![]() , are degenerate.
The shift in energy due to the magnetic field is simply
, are degenerate.
The shift in energy due to the magnetic field is simply
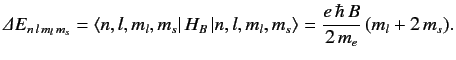
![]() states form two groups of four and
two states, depending on the values of their total angular momentum.
In the presence of an intense magnetic field, the
states form two groups of four and
two states, depending on the values of their total angular momentum.
In the presence of an intense magnetic field, the ![]() states are split
into five groups. There is a state with
states are split
into five groups. There is a state with
![]() ,
a state with
,
a state with
![]() , two states with
, two states with
![]() ,
a state with
,
a state with
![]() , and a state with
, and a state with
![]() . These groups are equally spaced in energy,
the energy difference between adjacent groups being
. These groups are equally spaced in energy,
the energy difference between adjacent groups being
![]() .
.
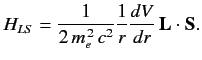
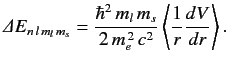
![]() states are split into five
groups with (
states are split into five
groups with (![]() ) quantum numbers
) quantum numbers ![]() ,
, ![]() ,
, ![]() or
or ![]() ,
, ![]() , and
, and ![]() , respectively, in order of
decreasing energy. The spin-orbit term increases the energy of
the highest energy state, does not affect the next highest energy state,
decreases, but does not split, the energy of the doublet, does
not affect the next lowest energy state, and increases
the energy of the lowest
energy state. The net result is that the five groups of states are no
longer equally spaced in energy.
, respectively, in order of
decreasing energy. The spin-orbit term increases the energy of
the highest energy state, does not affect the next highest energy state,
decreases, but does not split, the energy of the doublet, does
not affect the next lowest energy state, and increases
the energy of the lowest
energy state. The net result is that the five groups of states are no
longer equally spaced in energy.