


Next: Exercises
Up: Addition of Angular Momentum
Previous: Introduction
In order to answer this question, we need to learn how to add
angular momentum operators. Consider the most general case. Suppose
that we have two sets of angular momentum operators, 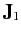 and
and 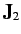 .
By definition, these operators are Hermitian, and obey the fundamental commutation
relations
.
By definition, these operators are Hermitian, and obey the fundamental commutation
relations
Let us assume that the two groups of operators correspond to different degrees
of freedom of the system, so that
![$\displaystyle [J_{1\,i}, J_{2\,j}] = 0,$](img1305.png) |
(545) |
where 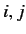 stand for either
stand for either  ,
, 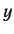 , or
, or  .
For instance,
.
For instance, 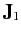 could be an orbital angular momentum operator, and
could be an orbital angular momentum operator, and 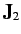 a spin angular momentum operator. Alternatively,
a spin angular momentum operator. Alternatively, 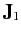 and
and 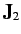 could
be the orbital angular momentum operators
of two different particles in a multi-particle
system. We know, from the general
properties of angular momentum, that the eigenvalues of
could
be the orbital angular momentum operators
of two different particles in a multi-particle
system. We know, from the general
properties of angular momentum, that the eigenvalues of  and
and  can be
written
can be
written
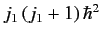 and
and
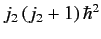 , respectively, where
, respectively, where
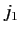 and
and  are either integers, or half-integers. We also know that the
eigenvalues of
are either integers, or half-integers. We also know that the
eigenvalues of 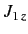 and
and 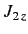 take the form
take the form
 and
and
 , respectively, where
, respectively, where  and
and 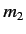 are numbers
lying in the ranges
are numbers
lying in the ranges
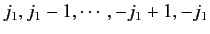 and
and
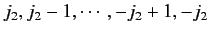 , respectively.
, respectively.
Let us define the total angular momentum operator
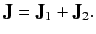 |
(546) |
Now, 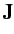 is an Hermitian operator, because it is the sum of Hermitian operators.
Moreover, according to Equations (300) and (303),
is an Hermitian operator, because it is the sum of Hermitian operators.
Moreover, according to Equations (300) and (303), 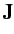 satisfies the fundamental commutation
relation
satisfies the fundamental commutation
relation
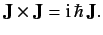 |
(547) |
Thus, 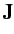 possesses all of the expected properties of an
angular momentum operator. It follows that the eigenvalue of
possesses all of the expected properties of an
angular momentum operator. It follows that the eigenvalue of 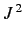 can be
written
can be
written
 , where
, where 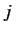 is an integer, or a half-integer. Moreover, the eigenvalue
of
is an integer, or a half-integer. Moreover, the eigenvalue
of  takes the form
takes the form  , where
, where  lies in the range
lies in the range
 . At this stage, however, we do not know the relationship between the quantum
numbers of the total angular momentum,
. At this stage, however, we do not know the relationship between the quantum
numbers of the total angular momentum, 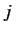 and
and  , and those of the
individual angular momenta,
, and those of the
individual angular momenta, 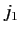 ,
,  ,
,  , and
, and 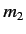 .
.
Now,
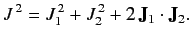 |
(548) |
Furthermore, we know that
and also that all of the 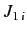 ,
,  operators commute with the
operators commute with the  ,
,  operators.
It follows from Equation (548) that
operators.
It follows from Equation (548) that
![$\displaystyle [J^{\,2}, J_1^{\,2}] = [J^{\,2}, J_2^{\,2}] = 0.$](img1332.png) |
(551) |
This implies that the quantum numbers 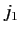 ,
,  , and
, and 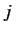 can all be measured
simultaneously. In other words, we can know the magnitude of the total
angular momentum together with the magnitudes of the component
angular momenta. However, it is apparent from Equation (548)
that
can all be measured
simultaneously. In other words, we can know the magnitude of the total
angular momentum together with the magnitudes of the component
angular momenta. However, it is apparent from Equation (548)
that
This suggests that it is not possible to measure the quantum numbers  and
and 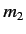 simultaneously with the quantum number
simultaneously with the quantum number 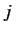 . Thus, we cannot determine
the projections of the individual angular momenta along the
. Thus, we cannot determine
the projections of the individual angular momenta along the  -axis
at the same time as the magnitude of the total angular momentum.
-axis
at the same time as the magnitude of the total angular momentum.
It is clear, from the preceding discussion, that we can form two alternate groups
of mutually commuting operators. The first group
is
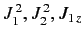 , and
, and
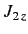 . The second group is
. The second group is
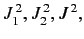 and
and  . These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
. These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
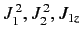 , and
, and
 are denoted
are denoted
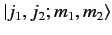 , where
, where
The simultaneous eigenkets of
 and
and  are denoted
are denoted
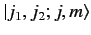 , where
, where
Each set of eigenkets are complete, mutually orthogonal (for eigenkets corresponding
to different sets of eigenvalues), and have unit norms. Since the operators
 and
and  are common to both operator groups, we can assume
that the quantum numbers
are common to both operator groups, we can assume
that the quantum numbers 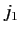 and
and  are known. In other words, we
can always determine
the magnitudes of the individual angular momenta. In addition, we can either
know the quantum numbers
are known. In other words, we
can always determine
the magnitudes of the individual angular momenta. In addition, we can either
know the quantum numbers  and
and 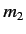 , or the quantum numbers
, or the quantum numbers 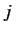 and
and
 , but we cannot know both pairs of quantum numbers at the same time.
We can write a conventional completeness relation for both sets of
eigenkets:
, but we cannot know both pairs of quantum numbers at the same time.
We can write a conventional completeness relation for both sets of
eigenkets:
where the right-hand sides denote the identity operator in the ket space corresponding
to states of given 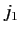 and
and  . The summation is over all allowed values
of
. The summation is over all allowed values
of  ,
, 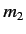 ,
, 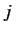 , and
, and  .
.
As we have seen, the operator group  ,
,  ,
, 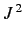 , and
, and  is incompatible with the group
is incompatible with the group  ,
,  ,
, 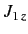 , and
, and 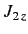 .
This means that if the system is in a simultaneous eigenstate of the former group
then, in general, it is not in an eigenstate of the latter. In other words,
if the quantum numbers
.
This means that if the system is in a simultaneous eigenstate of the former group
then, in general, it is not in an eigenstate of the latter. In other words,
if the quantum numbers 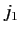 ,
,  ,
, 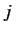 , and
, and  are known with
certainty then a measurement of the quantum numbers
are known with
certainty then a measurement of the quantum numbers  and
and 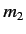 will
give a range of possible values. We can use the completeness relation
(562) to write
will
give a range of possible values. We can use the completeness relation
(562) to write
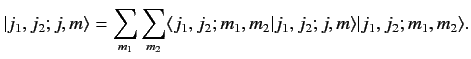 |
(564) |
Thus, we can write the eigenkets of the first group of operators
as a weighted sum of the eigenkets of the second set. The weights,
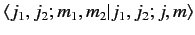 , are called the Clebsch-Gordon
coefficients. If the system is in a state where a measurement of
, are called the Clebsch-Gordon
coefficients. If the system is in a state where a measurement of
 , and
, and  is bound to give the results
is bound to give the results
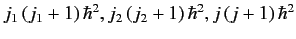 ,
and
,
and
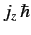 , respectively, then a measurement of
, respectively, then a measurement of 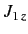 and
and 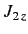 will give the results
will give the results
 and
and
 , respectively, with
probability
, respectively, with
probability
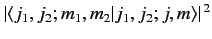 .
.
The Clebsch-Gordon coefficients possess a number of very important properties.
First, the coefficients are zero unless
 |
(565) |
To prove this, we note that
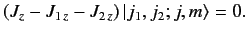 |
(566) |
Forming the inner product with
 , we obtain
, we obtain
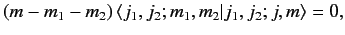 |
(567) |
which proves the assertion. Thus, the  -components of different angular momenta
add algebraically. So, an electron in an
-components of different angular momenta
add algebraically. So, an electron in an 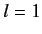 state, with orbital
angular momentum
state, with orbital
angular momentum 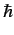 , and spin angular momentum
, and spin angular momentum 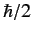 , projected along the
, projected along the
 -axis, constitutes a state whose total angular momentum projected
along the
-axis, constitutes a state whose total angular momentum projected
along the  -axis is
-axis is
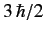 . What is uncertain is the magnitude of the
total angular momentum.
. What is uncertain is the magnitude of the
total angular momentum.
Second, the coefficients vanish unless
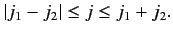 |
(568) |
We can assume, without loss of generality, that
 . We know,
from Equation (565), that for given
. We know,
from Equation (565), that for given
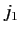 and
and  the largest possible value of
the largest possible value of  is
is 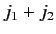 (because
(because
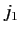 is the largest possible value of
is the largest possible value of  , etc.). This implies that
the largest possible value of
, etc.). This implies that
the largest possible value of 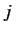 is
is 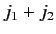 (since, by definition,
the largest value of
(since, by definition,
the largest value of  is equal to
is equal to 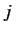 ).
Now, there are
).
Now, there are
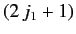 allowable values of
allowable values of  and
and
 allowable
values of
allowable
values of 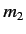 . Thus, there are
. Thus, there are
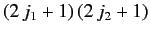 independent
eigenkets,
independent
eigenkets,
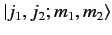 , needed to span the ket space
corresponding to fixed
, needed to span the ket space
corresponding to fixed 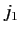 and
and  . Because the eigenkets
. Because the eigenkets
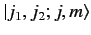 span the same space, they must also form
a set of
span the same space, they must also form
a set of
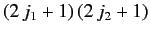 independent kets. In other words, there
can only be
independent kets. In other words, there
can only be
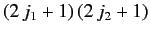 distinct allowable values of the quantum numbers
distinct allowable values of the quantum numbers
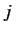 and
and  . For each allowed value of
. For each allowed value of 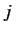 , there are
, there are 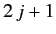 allowed values
of
allowed values
of  . We have already seen that the maximum allowed value of
. We have already seen that the maximum allowed value of 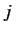 is
is
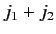 . It is easily seen that if the minimum allowed value of
. It is easily seen that if the minimum allowed value of
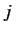 is
is 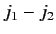 then the total number of allowed values of
then the total number of allowed values of 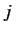 and
and  is
is
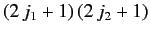 : i.e.,
: i.e.,
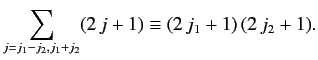 |
(569) |
This proves our assertion.
Third, the sum of the modulus squared of all of the Clebsch-Gordon coefficients
is unity: i.e.,
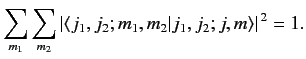 |
(570) |
This assertion is proved as follows:
where use has been made of the completeness relation (562).
Finally, the Clebsch-Gordon coefficients obey two recursion relations.
To obtain these relations, we start from
 |
(572) |
Making use of the well-known properties of the shift operators,
which are specified by Equations (344)-(345), we obtain
Taking the inner product with
 , and making
use of the orthonormality property of the basis eigenkets, we obtain
the desired recursion relations:
, and making
use of the orthonormality property of the basis eigenkets, we obtain
the desired recursion relations:
It is clear, from the absence of complex coupling coefficients in the above relations,
that we can always choose the Clebsch-Gordon coefficients to be real numbers.
This is convenient, because it ensures that the inverse Clebsch-Gordon
coefficients,
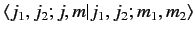 , are
identical to the Clebsch-Gordon coefficients. In other words,
, are
identical to the Clebsch-Gordon coefficients. In other words,
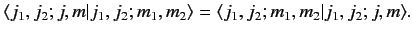 |
(575) |
The inverse Clebsch-Gordon coefficients are the weights in the expansion
of the
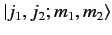 in terms of the
in terms of the
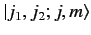 :
:
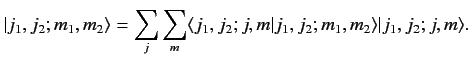 |
(576) |
It turns out that the recursion relations (574), together with the normalization
condition (570), are sufficient to completely determine the Clebsch-Gordon
coefficients to within an arbitrary sign (multiplied into
all of the coefficients). This sign is fixed by convention. The easiest
way of demonstrating this assertion is by considering a specific example.
Let us add the angular momentum of two spin one-half systems: e.g., two
electrons at rest. So,
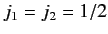 . We know, from general principles,
that
. We know, from general principles,
that
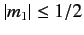 and
and
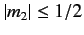 . We also know, from Equation (568),
that
. We also know, from Equation (568),
that
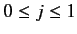 , where the allowed values of
, where the allowed values of 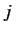 differ by integer amounts.
It follows that either
differ by integer amounts.
It follows that either 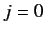 or
or 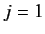 . Thus, two spin one-half systems can
be combined to form either a spin zero system or a spin one system.
It is helpful to arrange all of the possibly non-zero Clebsch-Gordon coefficients
in a table:
. Thus, two spin one-half systems can
be combined to form either a spin zero system or a spin one system.
It is helpful to arrange all of the possibly non-zero Clebsch-Gordon coefficients
in a table:
The box in this table corresponding to
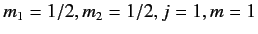 gives
the Clebsch-Gordon coefficient
gives
the Clebsch-Gordon coefficient
 ,
or the inverse Clebsch-Gordon coefficient
,
or the inverse Clebsch-Gordon coefficient
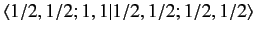 . All the boxes contain question marks because, at this stage, we do
not know the values of any Clebsch-Gordon coefficients.
. All the boxes contain question marks because, at this stage, we do
not know the values of any Clebsch-Gordon coefficients.
A Clebsch-Gordon coefficient is automatically zero unless
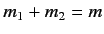 . In other words, the
. In other words, the  -components of angular momentum have to
add algebraically. Many of the boxes in the above table correspond to
-components of angular momentum have to
add algebraically. Many of the boxes in the above table correspond to
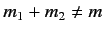 . We immediately conclude that these boxes must contain zeroes:
i.e.,
. We immediately conclude that these boxes must contain zeroes:
i.e.,
The normalization condition (570) implies that the sum of the squares
of all the rows and columns of the above table must be unity. There are two
rows and two columns that only contain a single non-zero entry. We conclude that
these entries must be 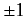 , but we have no way of determining the
signs at present. Thus,
, but we have no way of determining the
signs at present. Thus,
Let us evaluate the recursion relation (574) for
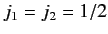 , with
, with
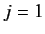 ,
, 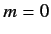 ,
,
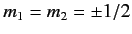 , taking the upper/lower sign. We
find that
, taking the upper/lower sign. We
find that
 |
(577) |
and
 |
(578) |
Here, the 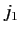 and
and  labels have been suppressed for ease of notation.
We also know that
labels have been suppressed for ease of notation.
We also know that
 |
(579) |
from the normalization condition. The only real solutions to the above set
of equations are
The choice of sign is arbitrary--the conventional choice is a positive
sign. Thus, our table now reads
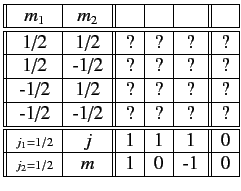
We could fill in the remaining unknown entries of our table by using the recursion
relation again. However, an easier method is to observe that the rows and columns
of the table must all be mutually orthogonal. That is, the dot product
of a row with any other row must be zero. Likewise, for the dot product of
a column with any other column. This follows because the entries in the
table give the expansion coefficients of one of our alternative sets of eigenkets
in terms of the other set, and each set of eigenkets contains
mutually orthogonal vectors with unit norms. The normalization
condition tells us that the dot product of a row or column with itself must
be unity. The only way that the dot product of the fourth column with
the second column can be zero is if the unknown entries are equal and opposite.
The requirement that the dot product of the fourth column with itself is
unity tells us that the magnitudes of the unknown entries have to be
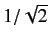 .
The unknown entries are undetermined to an arbitrary sign multiplied into them both.
Thus, the final form of our table (with the conventional choice of arbitrary
signs) is
.
The unknown entries are undetermined to an arbitrary sign multiplied into them both.
Thus, the final form of our table (with the conventional choice of arbitrary
signs) is

The table can be read in one of two ways. The columns give the expansions
of the eigenstates of overall angular momentum in terms of the eigenstates
of the individual
angular momenta of the two component systems. Thus, the second column
tells us that
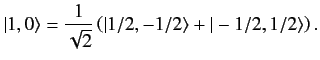 |
(581) |
The ket on the left-hand side is a
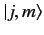 ket, whereas those on the
right-hand side are
ket, whereas those on the
right-hand side are
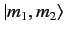 kets. The rows give the expansions
of the eigenstates of individual angular momentum in terms of those of overall
angular momentum. Thus, the second row tells us that
kets. The rows give the expansions
of the eigenstates of individual angular momentum in terms of those of overall
angular momentum. Thus, the second row tells us that
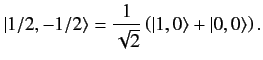 |
(582) |
Here, the ket on the left-hand side is a
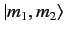 ket, whereas those
on the right-hand side are
ket, whereas those
on the right-hand side are
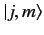 kets.
kets.
Note that our table is really a combination of two sub-tables, one involving
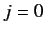 states, and one involving
states, and one involving 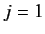 states. The Clebsch-Gordon coefficients
corresponding to two different choices of
states. The Clebsch-Gordon coefficients
corresponding to two different choices of 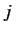 are completely independent:
i.e., there is no recursion relation linking Clebsch-Gordon coefficients
corresponding to different values of
are completely independent:
i.e., there is no recursion relation linking Clebsch-Gordon coefficients
corresponding to different values of 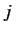 . Thus, for every choice of
. Thus, for every choice of 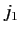 ,
,  ,
and
,
and 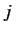 we can construct a table of Clebsch-Gordon coefficients corresponding
to the different allowed values of
we can construct a table of Clebsch-Gordon coefficients corresponding
to the different allowed values of  ,
, 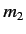 , and
, and  (subject to the
constraint that
(subject to the
constraint that 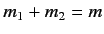 ). A complete knowledge of angular momentum addition
is equivalent to a knowing all possible tables of Clebsch-Gordon coefficients.
These tables are listed (for moderate values of
). A complete knowledge of angular momentum addition
is equivalent to a knowing all possible tables of Clebsch-Gordon coefficients.
These tables are listed (for moderate values of
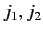 and
and 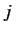 ) in many standard reference books.
) in many standard reference books.



Next: Exercises
Up: Addition of Angular Momentum
Previous: Introduction
Richard Fitzpatrick
2013-04-08
![]() , and
, and
![]() . The second group is
. The second group is
![]() and
and ![]() . These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
. These two
groups of operators are incompatible with one another. We can define simultaneous
eigenkets of each operator group. The simultaneous eigenkets of
![]() , and
, and
![]() are denoted
are denoted
![]() , where
, where
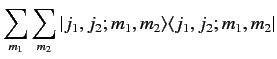
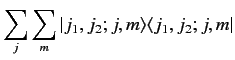
![]() ,
, ![]() ,
, ![]() , and
, and ![]() is incompatible with the group
is incompatible with the group ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
This means that if the system is in a simultaneous eigenstate of the former group
then, in general, it is not in an eigenstate of the latter. In other words,
if the quantum numbers
.
This means that if the system is in a simultaneous eigenstate of the former group
then, in general, it is not in an eigenstate of the latter. In other words,
if the quantum numbers ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are known with
certainty then a measurement of the quantum numbers
are known with
certainty then a measurement of the quantum numbers ![]() and
and ![]() will
give a range of possible values. We can use the completeness relation
(562) to write
will
give a range of possible values. We can use the completeness relation
(562) to write
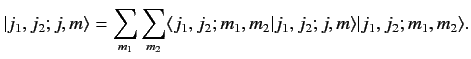
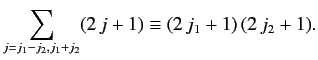
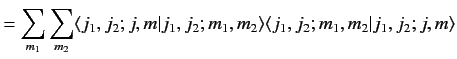


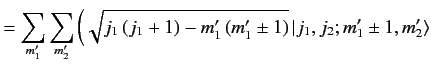

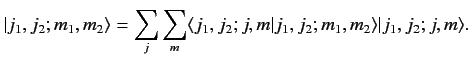
![]() . We know, from general principles,
that
. We know, from general principles,
that
![]() and
and
![]() . We also know, from Equation (568),
that
. We also know, from Equation (568),
that
![]() , where the allowed values of
, where the allowed values of ![]() differ by integer amounts.
It follows that either
differ by integer amounts.
It follows that either ![]() or
or ![]() . Thus, two spin one-half systems can
be combined to form either a spin zero system or a spin one system.
It is helpful to arrange all of the possibly non-zero Clebsch-Gordon coefficients
in a table:
. Thus, two spin one-half systems can
be combined to form either a spin zero system or a spin one system.
It is helpful to arrange all of the possibly non-zero Clebsch-Gordon coefficients
in a table:

![]() . In other words, the
. In other words, the ![]() -components of angular momentum have to
add algebraically. Many of the boxes in the above table correspond to
-components of angular momentum have to
add algebraically. Many of the boxes in the above table correspond to
![]() . We immediately conclude that these boxes must contain zeroes:
i.e.,
. We immediately conclude that these boxes must contain zeroes:
i.e.,

![]() , but we have no way of determining the
signs at present. Thus,
, but we have no way of determining the
signs at present. Thus,

![]() , with
, with
![]() ,
, ![]() ,
,
![]() , taking the upper/lower sign. We
find that
, taking the upper/lower sign. We
find that

![]() .
The unknown entries are undetermined to an arbitrary sign multiplied into them both.
Thus, the final form of our table (with the conventional choice of arbitrary
signs) is
.
The unknown entries are undetermined to an arbitrary sign multiplied into them both.
Thus, the final form of our table (with the conventional choice of arbitrary
signs) is

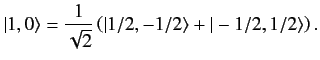
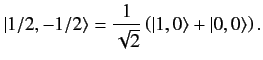
![]() states, and one involving
states, and one involving ![]() states. The Clebsch-Gordon coefficients
corresponding to two different choices of
states. The Clebsch-Gordon coefficients
corresponding to two different choices of ![]() are completely independent:
i.e., there is no recursion relation linking Clebsch-Gordon coefficients
corresponding to different values of
are completely independent:
i.e., there is no recursion relation linking Clebsch-Gordon coefficients
corresponding to different values of ![]() . Thus, for every choice of
. Thus, for every choice of ![]() ,
, ![]() ,
and
,
and ![]() we can construct a table of Clebsch-Gordon coefficients corresponding
to the different allowed values of
we can construct a table of Clebsch-Gordon coefficients corresponding
to the different allowed values of ![]() ,
, ![]() , and
, and ![]() (subject to the
constraint that
(subject to the
constraint that ![]() ). A complete knowledge of angular momentum addition
is equivalent to a knowing all possible tables of Clebsch-Gordon coefficients.
These tables are listed (for moderate values of
). A complete knowledge of angular momentum addition
is equivalent to a knowing all possible tables of Clebsch-Gordon coefficients.
These tables are listed (for moderate values of
![]() and
and ![]() ) in many standard reference books.
) in many standard reference books.