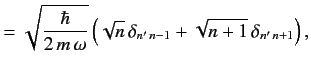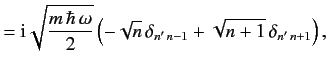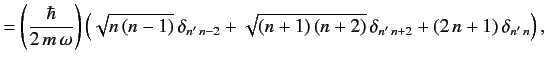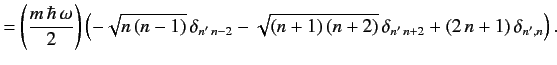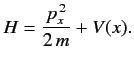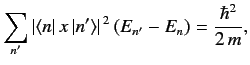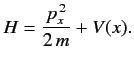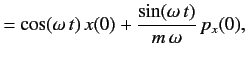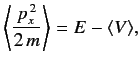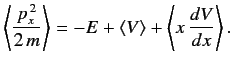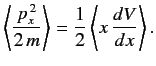Next: Orbital Angular Momentum
Up: Quantum Dynamics
Previous: Schrödinger Wave Equation
- Let
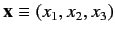 be a set of Cartesian position operators, and let
be a set of Cartesian position operators, and let
 be
the corresponding momentum operators. Demonstrate that
be
the corresponding momentum operators. Demonstrate that
where  , and
, and
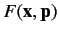 ,
,
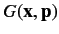 are functions that can be expanded as power series.
are functions that can be expanded as power series.
- Assuming that the potential
 is complex, demonstrate that the Schrödinger time-dependent wave equation, (274), can be transformed to give
is complex, demonstrate that the Schrödinger time-dependent wave equation, (274), can be transformed to give
where
and
- Consider one-dimensional quantum harmonic oscillator whose Hamiltonian is
where  and
and 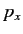 are conjugate position and momentum operators, respectively, and
are conjugate position and momentum operators, respectively, and  ,
, 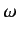 are
positive constants.
are
positive constants.
- Demonstrate that the expectation value of
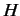 , for a general state, is
positive definite.
, for a general state, is
positive definite.
- Let
Deduce that
- Suppose that
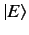 is an eigenket of the Hamiltonian whose corresponding energy is
is an eigenket of the Hamiltonian whose corresponding energy is 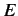 : i.e.,
: i.e.,
Demonstrate that
Hence, deduce that the allowed values of 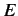 are
are
where
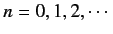 .
.
- Let
 be a properly normalized (i.e.,
be a properly normalized (i.e.,
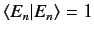 ) energy eigenket corresponding to the
eigenvalue
) energy eigenket corresponding to the
eigenvalue 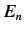 . Show that the kets can be defined such that
. Show that the kets can be defined such that
Hence, deduce that
- Let the
 be the wavefunctions of the properly normalized energy eigenkets.
Given that
be the wavefunctions of the properly normalized energy eigenkets.
Given that
deduce that
where
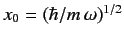 . Hence, show that
. Hence, show that
- Consider the one-dimensional quantum harmonic oscillator discussed in Exercise 3. Let
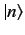 be
a properly normalized energy eigenket belonging to the eigenvalue
be
a properly normalized energy eigenket belonging to the eigenvalue 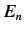 . Show that
. Show that
Hence, deduce that
for the 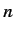 th eigenstate.
th eigenstate.
- Consider a particle in one dimension whose Hamiltonian is
By calculating
![$ [[H,x], x]$](img707.png) , demonstrate that
, demonstrate that
where 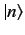 is a properly normalized energy eigenket corresponding to the eigenvalue
is a properly normalized energy eigenket corresponding to the eigenvalue 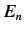 , and the
sum is over all eigenkets.
, and the
sum is over all eigenkets.
- Consider a particle in one dimension whose Hamiltonian is
Suppose that the potential is periodic, such that
for all  . Deduce that
. Deduce that
where 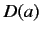 is the displacement operator defined in Exercise 4. Hence, show that the wavefunction of
an energy eigenstate has the general form
is the displacement operator defined in Exercise 4. Hence, show that the wavefunction of
an energy eigenstate has the general form
where 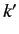 is a real parameter, and
is a real parameter, and
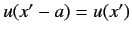 for all
for all 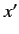 . This result is known as the Bloch theorem.
. This result is known as the Bloch theorem.
- Consider the one-dimensional quantum harmonic oscillator discussed in Exercise 3. Show that the Heisenberg equations of motion of the ladder operators
 and
and 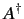 are
are
respectively.
Hence, deduce that the momentum and position operators evolve in time as
respectively, in the Heisenberg picture.
- Consider a one-dimensional stationary bound state. Using the time-independent Schrödinger equation,
prove that
and
[Hint: You can assume, without loss of generality, that the stationary wavefunction is real.] Hence, prove the Virial
theorem,



Next: Orbital Angular Momentum
Up: Quantum Dynamics
Previous: Schrödinger Wave Equation
Richard Fitzpatrick
2013-04-08
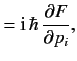
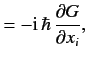

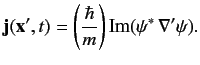
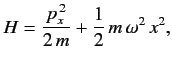
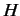 , for a general state, is
positive definite.
, for a general state, is
positive definite.
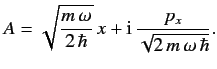
![$\displaystyle [A,A^\dag ]$](img666.png)
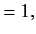

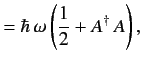
![$\displaystyle [H,A]$](img670.png)
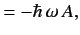
![$\displaystyle [H,A^\dag ]$](img672.png)
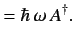
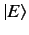 is an eigenket of the Hamiltonian whose corresponding energy is
is an eigenket of the Hamiltonian whose corresponding energy is 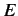 : i.e.,
: i.e.,
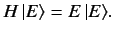
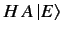

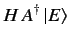
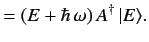
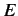 are
are
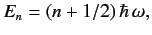
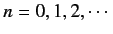 .
.
 be a properly normalized (i.e.,
be a properly normalized (i.e.,
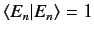 ) energy eigenket corresponding to the
eigenvalue
) energy eigenket corresponding to the
eigenvalue 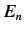 . Show that the kets can be defined such that
. Show that the kets can be defined such that
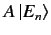
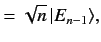

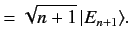
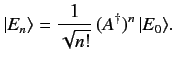
 be the wavefunctions of the properly normalized energy eigenkets.
Given that
be the wavefunctions of the properly normalized energy eigenkets.
Given that
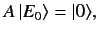
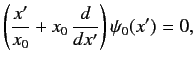
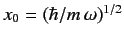 . Hence, show that
. Hence, show that
![$\displaystyle \psi_n(x') = \frac{1}{\pi^{1/4}\,(2^n\,n!)^{1/2}\,x_0^{\,n+1/2}}\...
...c{d}{dx'}\right)^n\exp\left[-\frac{1}{2}\left(
\frac{x'}{x_0}\right)^2\right].
$](img695.png)