where
where
![$\displaystyle \psi(x') =\psi_0\,\exp\left[-\frac{(x'-x_0)^{\,2}}{4\,\sigma^2}\right],
$](img504.png)
where
where
[Hint: Use the momentum representation,
Hence, deduce that
where
Let
![]() , and let
, and let
![]() denote an eigenket of the
denote an eigenket of the ![]() operator belonging to the eigenvalue
operator belonging to the eigenvalue ![]() .
Demonstrate that
.
Demonstrate that
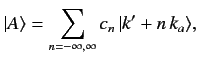
where the
where
![$\displaystyle \psi(x') =\psi_0\,\exp\left[-\frac{(x'-x_0)^{\,2}}{4\,\sigma^2}\right],
$](img504.png)
where

where
[Hint: Use the momentum representation,
Hence, deduce that
where
Let
![]() , and let
, and let
![]() denote an eigenket of the
denote an eigenket of the ![]() operator belonging to the eigenvalue
operator belonging to the eigenvalue ![]() .
Demonstrate that
.
Demonstrate that
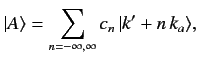
where the
where