


Next: Exercises
Up: Position and Momentum
Previous: Uncertainty Relation
Displacement Operators
Consider a system with one degree of freedom corresponding to the Cartesian
coordinate  . Suppose that we displace this system some distance along the
. Suppose that we displace this system some distance along the  -axis.
We could imagine that the system is on wheels, and we just give it a little
push. The final state of the system is completely determined by its initial state,
together with the direction and magnitude of the displacement.
Note that the type of displacement we are considering is one in which
everything to do with the system is displaced. So, if the system is
subject to an external potential then the potential must be displaced.
-axis.
We could imagine that the system is on wheels, and we just give it a little
push. The final state of the system is completely determined by its initial state,
together with the direction and magnitude of the displacement.
Note that the type of displacement we are considering is one in which
everything to do with the system is displaced. So, if the system is
subject to an external potential then the potential must be displaced.
The situation is not so clear with state kets. The final state
of the system only determines the direction of the displaced state ket. Even if
we adopt the convention that all state kets have unit norms, the final ket is
still not completely determined, because it can be multiplied by a constant phase-factor. However, we know that the superposition relations between states
remain invariant under the displacement. This follows because the superposition
relations have a physical significance that is unaffected by a displacement of
the system.
Thus, if
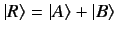 |
(194) |
in the undisplaced system, and the displacement causes ket  to
transform to ket
to
transform to ket
 , etc., then in the displaced system we have
, etc., then in the displaced system we have
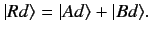 |
(195) |
Incidentally, this determines the displaced kets to within a single arbitrary phase-factor to be multiplied into all of them. The displaced kets cannot be multiplied by
individual phase-factors, because this would wreck the superposition relations.
Since Equation (195) holds in the displaced system whenever Equation (194) holds in the
undisplaced system, it follows that the displaced ket
 must be the
result of some linear operator acting on the undisplaced ket
must be the
result of some linear operator acting on the undisplaced ket
 . In other
words,
. In other
words,
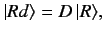 |
(196) |
where 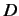 an operator that depends only on the
nature of the displacement. The arbitrary phase-factor by which all
displaced kets may be multiplied results in
an operator that depends only on the
nature of the displacement. The arbitrary phase-factor by which all
displaced kets may be multiplied results in 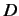 being undetermined to an arbitrary
multiplicative constant of modulus unity.
being undetermined to an arbitrary
multiplicative constant of modulus unity.
We now adopt the ansatz that any combination of bras, kets, and dynamical
variables that possesses a physical significance is invariant under a displacement
of the system. The normalization condition
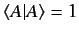 |
(197) |
for a state ket  certainly has a physical significance. Thus, we must
have
certainly has a physical significance. Thus, we must
have
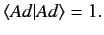 |
(198) |
Now,
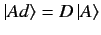 and
and
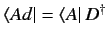 , so
, so
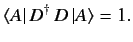 |
(199) |
Because this must hold for any state ket  , it follows that
, it follows that
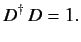 |
(200) |
Hence, the displacement operator is unitary.
Note that the above relation implies that
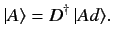 |
(201) |
The equation
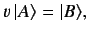 |
(202) |
where the operator
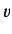 represents a dynamical variable, has some physical significance. Thus,
we require that
represents a dynamical variable, has some physical significance. Thus,
we require that
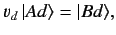 |
(203) |
where 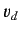 is the displaced operator. It follows that
is the displaced operator. It follows that
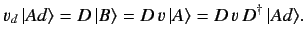 |
(204) |
Since this is true for any ket
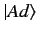 , we have
, we have
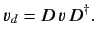 |
(205) |
Note that the arbitrary numerical factor in 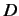 does not affect either of the
results (200) and (205).
does not affect either of the
results (200) and (205).
Suppose, now, that the system is displaced an infinitesimal distance 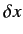 along the
along the  -axis. We expect that the displaced ket
-axis. We expect that the displaced ket
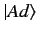 should
approach the undisplaced ket
should
approach the undisplaced ket
 in the limit as
in the limit as
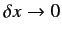 . Thus,
we expect the limit
. Thus,
we expect the limit
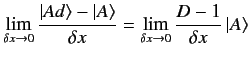 |
(206) |
to exist. Let
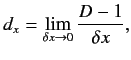 |
(207) |
where 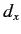 is denoted the displacement operator along the
is denoted the displacement operator along the  -axis. The fact
that
-axis. The fact
that 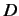 can be replaced by
can be replaced by
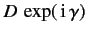 , where
, where 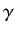 is a real
phase-angle, implies that
is a real
phase-angle, implies that 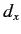 can be replaced by
can be replaced by
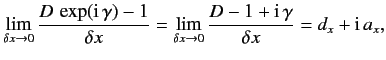 |
(208) |
where 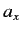 is the limit of
is the limit of
 . We have assumed, as seems
reasonable, that
. We have assumed, as seems
reasonable, that 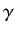 tends
to zero as
tends
to zero as
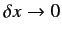 . It is clear that the displacement operator
is undetermined to an arbitrary imaginary additive constant.
. It is clear that the displacement operator
is undetermined to an arbitrary imaginary additive constant.
For small 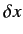 , we have
, we have
 |
(209) |
It follows from Equation (200) that
 |
(210) |
Neglecting order
 , we obtain
, we obtain
 |
(211) |
Thus, the displacement operator is anti-Hermitian. Substituting into
Equation (205), and again neglecting order
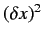 , we find that
, we find that
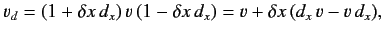 |
(212) |
which implies
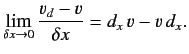 |
(213) |
Let us consider a specific example.
Suppose that a state has a wavefunction 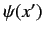 . If the system is displaced
a distance
. If the system is displaced
a distance 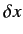 along the
along the  -axis then the new wavefunction is
-axis then the new wavefunction is
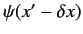 (i.e., the same shape shifted in the
(i.e., the same shape shifted in the  -direction
by a distance
-direction
by a distance 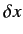 ). Actually, the new wavefunction can be multiplied by
an arbitrary number of modulus unity. It can be seen that the new wavefunction
is obtained from the old wavefunction according to the
prescription
). Actually, the new wavefunction can be multiplied by
an arbitrary number of modulus unity. It can be seen that the new wavefunction
is obtained from the old wavefunction according to the
prescription
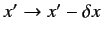 . Thus,
. Thus,
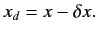 |
(214) |
A comparison with Equation (213), using 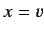 , yields
, yields
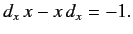 |
(215) |
It follows that
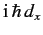 obeys the same commutation relation with
obeys the same commutation relation with
 that
that 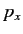 , the momentum conjugate to
, the momentum conjugate to  , does [see Equation (116)].
The most general conclusion we can draw from this observation is that
, does [see Equation (116)].
The most general conclusion we can draw from this observation is that
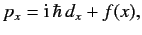 |
(216) |
where 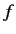 is Hermitian (since
is Hermitian (since 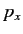 is Hermitian). However, the fact that
is Hermitian). However, the fact that 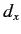 is undetermined to an arbitrary additive imaginary constant (which could be a function
of
is undetermined to an arbitrary additive imaginary constant (which could be a function
of  ) enables us to transform the function
) enables us to transform the function 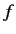 out of the above equation, leaving
out of the above equation, leaving
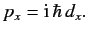 |
(217) |
Thus, the displacement operator in the  -direction is proportional to the
momentum conjugate to
-direction is proportional to the
momentum conjugate to  . We say that
. We say that 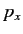 is the generator of translations
along the
is the generator of translations
along the  -axis.
-axis.
A finite translation along the  -axis can be constructed from
a series of very many
infinitesimal translations. Thus, the operator
-axis can be constructed from
a series of very many
infinitesimal translations. Thus, the operator
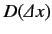 which translates the
system a distance
which translates the
system a distance
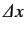 along the
along the  -axis is
written
-axis is
written
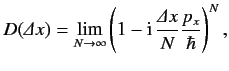 |
(218) |
where use has been made of Equations (209) and (217). It follows that
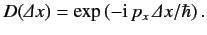 |
(219) |
The unitary nature of the operator is now clearly apparent.
We can also construct displacement operators which translate the system along
the 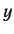 - and
- and  -axes. Note that a displacement a distance
-axes. Note that a displacement a distance
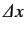 along the
along the
 -axis commutes with a displacement a distance
-axis commutes with a displacement a distance
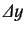 along the
along the
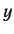 -axis.
In other words, if the system is moved
-axis.
In other words, if the system is moved
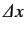 along the
along the  -axis, and then
-axis, and then
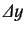 along the
along the 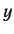 -axis, then it ends up in the same state as if it were moved
-axis, then it ends up in the same state as if it were moved
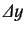 along the
along the 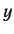 -axis, and then
-axis, and then
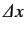 along the
along the  -axis. The fact that
translations in independent directions commute is clearly associated with the
fact that the conjugate momentum operators
associated with these directions also commute
[see Equations (115) and (219)].
-axis. The fact that
translations in independent directions commute is clearly associated with the
fact that the conjugate momentum operators
associated with these directions also commute
[see Equations (115) and (219)].



Next: Exercises
Up: Position and Momentum
Previous: Uncertainty Relation
Richard Fitzpatrick
2013-04-08
![]() must be the
result of some linear operator acting on the undisplaced ket
must be the
result of some linear operator acting on the undisplaced ket
![]() . In other
words,
. In other
words,
![]() along the
along the ![]() -axis. We expect that the displaced ket
-axis. We expect that the displaced ket
![]() should
approach the undisplaced ket
should
approach the undisplaced ket
![]() in the limit as
in the limit as
![]() . Thus,
we expect the limit
. Thus,
we expect the limit
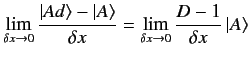
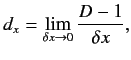
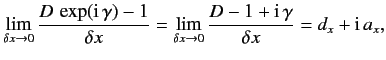
![]() , we have
, we have
![]() . If the system is displaced
a distance
. If the system is displaced
a distance ![]() along the
along the ![]() -axis then the new wavefunction is
-axis then the new wavefunction is
![]() (i.e., the same shape shifted in the
(i.e., the same shape shifted in the ![]() -direction
by a distance
-direction
by a distance ![]() ). Actually, the new wavefunction can be multiplied by
an arbitrary number of modulus unity. It can be seen that the new wavefunction
is obtained from the old wavefunction according to the
prescription
). Actually, the new wavefunction can be multiplied by
an arbitrary number of modulus unity. It can be seen that the new wavefunction
is obtained from the old wavefunction according to the
prescription
![]() . Thus,
. Thus,
![]() -axis can be constructed from
a series of very many
infinitesimal translations. Thus, the operator
-axis can be constructed from
a series of very many
infinitesimal translations. Thus, the operator
![]() which translates the
system a distance
which translates the
system a distance
![]() along the
along the ![]() -axis is
written
-axis is
written
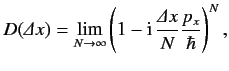
![]() - and
- and ![]() -axes. Note that a displacement a distance
-axes. Note that a displacement a distance
![]() along the
along the
![]() -axis commutes with a displacement a distance
-axis commutes with a displacement a distance
![]() along the
along the
![]() -axis.
In other words, if the system is moved
-axis.
In other words, if the system is moved
![]() along the
along the ![]() -axis, and then
-axis, and then
![]() along the
along the ![]() -axis, then it ends up in the same state as if it were moved
-axis, then it ends up in the same state as if it were moved
![]() along the
along the ![]() -axis, and then
-axis, and then
![]() along the
along the ![]() -axis. The fact that
translations in independent directions commute is clearly associated with the
fact that the conjugate momentum operators
associated with these directions also commute
[see Equations (115) and (219)].
-axis. The fact that
translations in independent directions commute is clearly associated with the
fact that the conjugate momentum operators
associated with these directions also commute
[see Equations (115) and (219)].