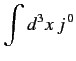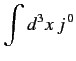Next: About this document ...
Up: Relativistic Electron Theory
Previous: Positron Theory
- Noting that
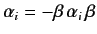 , prove that the
, prove that the 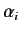 and
and 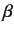 matrices all have zero trace. Hence,
deduce that each of these matrices has
matrices all have zero trace. Hence,
deduce that each of these matrices has 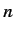 eigenvalues
eigenvalues 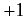 , and
, and 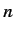 eigenvalues
eigenvalues 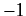 , where
, where  is the dimension
of the matrices.
is the dimension
of the matrices.
- Verify that the matrices (1125) and (1126) satisfy Equations (1117)-(1119).
- Verify that the matrices (1123) and (1124) satisfy the anti-commutation relations (1122).
- Verify that if
where 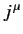 is a 4-vector field, then
is a 4-vector field, then
is Lorentz invariant, where the integral is over all space, and it is assumed that
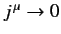 as
as
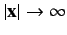 .
.
- Verify that (1168) is a solution of (1167).
- Verify that the
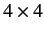 matrices
matrices 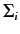 , defined in (1189), satisfy the standard anti-commutation
relations for Pauli matrices: i.e.,
, defined in (1189), satisfy the standard anti-commutation
relations for Pauli matrices: i.e.,
Richard Fitzpatrick
2013-04-08