


Next: Free Electron Motion
Up: Relativistic Electron Theory
Previous: Dirac Equation
Consider two inertial frames, 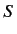 and
and  . Let the
. Let the 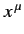 and
and
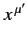 be the space-time coordinates of a given event in each frame, respectively.
These coordinates are related via a Lorentz transformation, which takes the general form
be the space-time coordinates of a given event in each frame, respectively.
These coordinates are related via a Lorentz transformation, which takes the general form
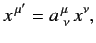 |
(1145) |
where the
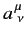 are real numerical coefficients that are independent of the
are real numerical coefficients that are independent of the 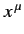 .
We also have
.
We also have
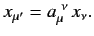 |
(1146) |
Now, since [see Equation (1102)]
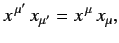 |
(1147) |
it follows that
 |
(1148) |
Moreover, it is easily shown that
By definition, a 4-vector 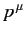 has analogous transformation properties to the
has analogous transformation properties to the 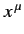 . Thus,
. Thus,
etc.
In frame 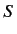 , the Dirac equation is written
, the Dirac equation is written
![$\displaystyle \left[\gamma^{\,\mu}\left(p_\mu- \frac{e}{c}\,{\mit\Phi}_\mu\right)-m_e\,c\right]\psi = 0.$](img2669.png) |
(1153) |
Let 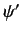 be the wavefunction in frame
be the wavefunction in frame  . Suppose that
. Suppose that
 |
(1154) |
where  is a
is a 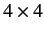 transformation matrix that is independent of the
transformation matrix that is independent of the 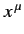 . (Hence,
. (Hence,  commutes with the
commutes with the 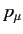 and the
and the
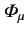 .)
Multiplying (1153) by
.)
Multiplying (1153) by  , we obtain
, we obtain
![$\displaystyle \left[A\,\gamma^{\,\mu}\,A^{-1}\left(p_\mu- \frac{e}{c}\,{\mit\Phi}_\mu\right)-m_e\,c\right]\psi' = 0.$](img2674.png) |
(1155) |
Hence, given that the 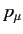 and
and
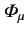 are the covariant components of 4-vectors, we obtain
are the covariant components of 4-vectors, we obtain
![$\displaystyle \left[A\,\gamma^{\,\mu}\,A^{-1}\,a^\nu_{~\mu}\left(p_{\nu'}- \frac{e}{c}\,{\mit\Phi}_{\nu'}\right)-m_e\,c\right]\psi' = 0.$](img2675.png) |
(1156) |
Suppose that
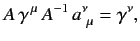 |
(1157) |
which is equivalent to
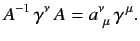 |
(1158) |
Here, we have assumed that the
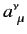 commute with
commute with  and the
and the
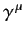 (since they are just numbers). If (1157)
holds then (1156) becomes
(since they are just numbers). If (1157)
holds then (1156) becomes
![$\displaystyle \left[\gamma^{\,\mu}\left(p_{\mu'}- \frac{e}{c}\,{\mit\Phi}_{\mu'}\right)-m_e\,c\right]\psi' = 0.$](img2679.png) |
(1159) |
A comparison of this equation with (1153) reveals that the Dirac equation takes the same form in frames 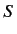 and
and  . In other words, the
Dirac equation is Lorentz invariant. Incidentally, it is clear from (1153) and (1159) that the
. In other words, the
Dirac equation is Lorentz invariant. Incidentally, it is clear from (1153) and (1159) that the
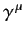 matrices are
the same in all inertial frames.
matrices are
the same in all inertial frames.
It remains to find a transformation matrix  that satisfies (1158). Consider an infinitesimal Lorentz transformation, for which
that satisfies (1158). Consider an infinitesimal Lorentz transformation, for which
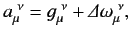 |
(1160) |
where the
 are real numerical coefficients that are independent of the
are real numerical coefficients that are independent of the 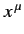 , and are also small compared to unity. To first order in small quantities, (1148) yields
, and are also small compared to unity. To first order in small quantities, (1148) yields
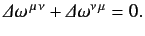 |
(1161) |
Let us write
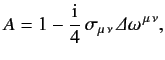 |
(1162) |
where the
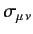 are
are
 matrices. To first order in small
quantities,
matrices. To first order in small
quantities,
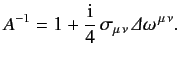 |
(1163) |
Moreover, it follows from (1161) that
 |
(1164) |
To first order in small quantities, Equations (1158), (1160), (1162), and (1163) yield
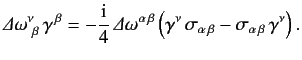 |
(1165) |
Hence, making use of the symmetry property (1161), we obtain
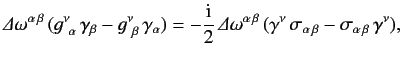 |
(1166) |
where
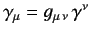 .
Since this equation must hold for arbitrary
.
Since this equation must hold for arbitrary
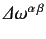 , we deduce that
, we deduce that
![$\displaystyle 2\,{\rm i}\,(g^\nu_{~\alpha}\,\gamma_\beta -g^\nu_{~\beta}\,\gamma_\alpha) = [\gamma^\nu, \sigma_{\alpha\,\beta}].$](img2692.png) |
(1167) |
Making use of the anti-commutation relations (1122), it can be shown that a suitable solution of the above
equation is
![$\displaystyle \sigma_{\mu\,\nu} = \frac{{\rm i}}{2}\,[\gamma_\mu,\gamma_\nu].$](img2693.png) |
(1168) |
Hence,
Now that we have found the correct transformation rules for an infinitesimal Lorentz transformation, we can easily find those for a
finite transformation by building it up from a large number of successive infinitesimal transforms.
Making use of (1127), as well as
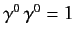 , the Hermitian conjugate of (1169) can be shown
to take the form
, the Hermitian conjugate of (1169) can be shown
to take the form
![$\displaystyle A^\dag = 1-\frac{1}{8}\,\gamma^0\,[\gamma_\mu,\gamma_\nu]\,\gamma^0\,{\mit\Delta}\omega^{\,\mu\,\nu} = \gamma^0\,A^{-1}\,\gamma^0.$](img2699.png) |
(1171) |
Hence, (1158) yields
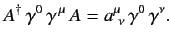 |
(1172) |
It follows that
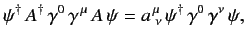 |
(1173) |
or
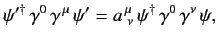 |
(1174) |
which implies that
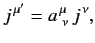 |
(1175) |
where the 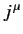 are defined in Equation (1139). This proves that the
are defined in Equation (1139). This proves that the 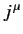 transform as the contravariant components
of a 4-vector.
transform as the contravariant components
of a 4-vector.



Next: Free Electron Motion
Up: Relativistic Electron Theory
Previous: Dirac Equation
Richard Fitzpatrick
2013-04-08
![]() , the Dirac equation is written
, the Dirac equation is written
![$\displaystyle \left[A\,\gamma^{\,\mu}\,A^{-1}\left(p_\mu- \frac{e}{c}\,{\mit\Phi}_\mu\right)-m_e\,c\right]\psi' = 0.$](img2674.png)
![]() that satisfies (1158). Consider an infinitesimal Lorentz transformation, for which
that satisfies (1158). Consider an infinitesimal Lorentz transformation, for which
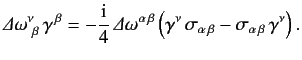
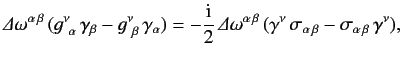
![$\displaystyle = 1 + \frac{1}{8}\,[\gamma_\mu,\gamma_\nu]\,{\mit\Delta}\omega^{\,\mu\,\nu},$](img2695.png)
![$\displaystyle = 1 - \frac{1}{8}\,[\gamma_\mu,\gamma_\nu]\,{\mit\Delta}\omega^{\,\mu\,\nu}.$](img2697.png)
![]() , the Hermitian conjugate of (1169) can be shown
to take the form
, the Hermitian conjugate of (1169) can be shown
to take the form
![$\displaystyle A^\dag = 1-\frac{1}{8}\,\gamma^0\,[\gamma_\mu,\gamma_\nu]\,\gamma^0\,{\mit\Delta}\omega^{\,\mu\,\nu} = \gamma^0\,A^{-1}\,\gamma^0.$](img2699.png)