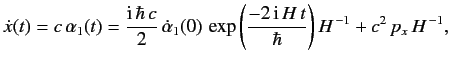Next: Electron Spin
Up: Relativistic Electron Theory
Previous: Lorentz Invariance of Dirac
According to Equation (1129), the relativistic Hamiltonian of a free electron takes the form
Let us use the Heisenberg picture to investigate the motion of such an electron. For the
sake of brevity, we shall omit the suffix 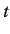 that should be appended to dynamical variables that vary in time, according to the formalism of Section 3.2.
that should be appended to dynamical variables that vary in time, according to the formalism of Section 3.2.
The above Hamiltonian is independent of 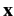 . Hence, momentum
. Hence, momentum 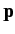 commutes with the Hamiltonian, and is therefore a
constant of the motion. The
commutes with the Hamiltonian, and is therefore a
constant of the motion. The  component of the velocity is
component of the velocity is
![$\displaystyle \dot{x} = \frac{[x,H]}{{\rm i}\,\hbar} = c\,\alpha_1,$](img2706.png) |
(1177) |
where use has been made of the standard commutation relations between position and momentum operators.
This result is rather surprising, since it implies a relationship between velocity and momentum that is quite different from that
in classical mechanics. This relationship, however, is clearly connected to the expression
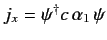 for the
for the
 component of the probability current. The operator
component of the probability current. The operator 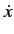 , specified in the above equation, has the eigenvalues
, specified in the above equation, has the eigenvalues 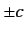 ,
corresponding to the eigenvalues
,
corresponding to the eigenvalues 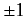 of
of  . Since
. Since 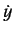 and
and 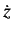 are similar to
are similar to 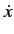 , we
conclude that a measurement of a velocity component of a free electron is certain to yield the result
, we
conclude that a measurement of a velocity component of a free electron is certain to yield the result 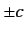 . As is easily demonstrated, this conclusion also
holds in the presence of an electromagnetic field.
. As is easily demonstrated, this conclusion also
holds in the presence of an electromagnetic field.
Of course, electrons are often observed to have velocities considerably less than that of light. Hence, the previous conclusion seems to
be in conflict with experimental observations. The conflict is not real, however, because the theoretical velocity discussed above is
the velocity at one instance in time, whereas observed velocities are always averages over a finite time interval. We shall find, on
further examination of the equations of motion, that the velocity of a free electron is not constant, but oscillates rapidly about a mean value
that agrees with the experimentally observed value.
In order to understand why a measurement of a velocity component must lead to the result 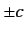 in a relativistic theory, consider the
following argument. To measure the velocity we must measure the position at two slightly different times, and then divide the
change in position by the time interval. (We cannot just measure the momentum and then apply a formula, because the
ordinary connection between velocity and momentum is no longer valid.) In order that our measured velocity may
approximate to the instantaneous velocity, the time interval between the two measurements of position must be very short, and the
measurements themselves very accurate. However, the great accuracy with which the position of the electron
is known during the time interval leads to an almost complete indeterminacy in its momentum, according to the Heisenberg uncertainty principle.
This means that almost all values of the momentum are equally likely, so that the momentum is almost certain to be infinite. But, an infinite
value of a momentum component corresponds to the values
in a relativistic theory, consider the
following argument. To measure the velocity we must measure the position at two slightly different times, and then divide the
change in position by the time interval. (We cannot just measure the momentum and then apply a formula, because the
ordinary connection between velocity and momentum is no longer valid.) In order that our measured velocity may
approximate to the instantaneous velocity, the time interval between the two measurements of position must be very short, and the
measurements themselves very accurate. However, the great accuracy with which the position of the electron
is known during the time interval leads to an almost complete indeterminacy in its momentum, according to the Heisenberg uncertainty principle.
This means that almost all values of the momentum are equally likely, so that the momentum is almost certain to be infinite. But, an infinite
value of a momentum component corresponds to the values 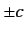 for the corresponding velocity component.
for the corresponding velocity component.
Let us now examine how the election velocity varies in time. We have
 |
(1178) |
Now  anti-commutes with all terms in
anti-commutes with all terms in 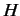 except
except
 ,
so
,
so
 |
(1179) |
Here, use has been made of the fact that  commutes with
commutes with 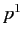 , and also that
, and also that
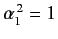 .
Hence, we get
.
Hence, we get
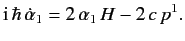 |
(1180) |
Since 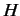 and
and 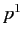 are constants of the motion, this equation yields
are constants of the motion, this equation yields
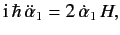 |
(1181) |
which can be integrated to give
 |
(1182) |
It follows from Equation (1177) and (1180) that
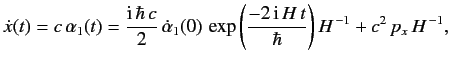 |
(1183) |
and
 |
(1184) |
We can see that the  -component of velocity consists of two parts, a constant part,
-component of velocity consists of two parts, a constant part,
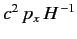 , connected with the momentum
according to the classical relativistic formula, and an oscillatory part whose frequency,
, connected with the momentum
according to the classical relativistic formula, and an oscillatory part whose frequency, 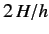 , is high (being at least
, is high (being at least
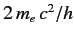 ).
Only the constant part would be observed in a practical measurement of velocity (i.e., an average over a short time interval that is still much longer than
).
Only the constant part would be observed in a practical measurement of velocity (i.e., an average over a short time interval that is still much longer than
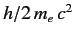 ).
The oscillatory part ensures that the instantaneous value of
).
The oscillatory part ensures that the instantaneous value of 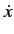 has the eigenvalues
has the eigenvalues 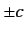 . Note, finally, that the oscillatory part of
. Note, finally, that the oscillatory part of  is small, being of
order
is small, being of
order
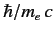 .
.



Next: Electron Spin
Up: Relativistic Electron Theory
Previous: Lorentz Invariance of Dirac
Richard Fitzpatrick
2013-04-08
![]() . Hence, momentum
. Hence, momentum ![]() commutes with the Hamiltonian, and is therefore a
constant of the motion. The
commutes with the Hamiltonian, and is therefore a
constant of the motion. The ![]() component of the velocity is
component of the velocity is
![]() in a relativistic theory, consider the
following argument. To measure the velocity we must measure the position at two slightly different times, and then divide the
change in position by the time interval. (We cannot just measure the momentum and then apply a formula, because the
ordinary connection between velocity and momentum is no longer valid.) In order that our measured velocity may
approximate to the instantaneous velocity, the time interval between the two measurements of position must be very short, and the
measurements themselves very accurate. However, the great accuracy with which the position of the electron
is known during the time interval leads to an almost complete indeterminacy in its momentum, according to the Heisenberg uncertainty principle.
This means that almost all values of the momentum are equally likely, so that the momentum is almost certain to be infinite. But, an infinite
value of a momentum component corresponds to the values
in a relativistic theory, consider the
following argument. To measure the velocity we must measure the position at two slightly different times, and then divide the
change in position by the time interval. (We cannot just measure the momentum and then apply a formula, because the
ordinary connection between velocity and momentum is no longer valid.) In order that our measured velocity may
approximate to the instantaneous velocity, the time interval between the two measurements of position must be very short, and the
measurements themselves very accurate. However, the great accuracy with which the position of the electron
is known during the time interval leads to an almost complete indeterminacy in its momentum, according to the Heisenberg uncertainty principle.
This means that almost all values of the momentum are equally likely, so that the momentum is almost certain to be infinite. But, an infinite
value of a momentum component corresponds to the values ![]() for the corresponding velocity component.
for the corresponding velocity component.