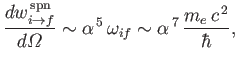Next: Photo-Ionization
Up: Time-Dependent Perturbation Theory
Previous: Magnetic Dipole Transitions
According to Equation (8.195), the quantity that mediates spontaneous electric quadrupole
transitions is
where
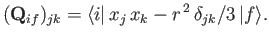 |
(8.213) |
is the electric quadrupole matrix element. It follows,
by analogy with with Equation (8.165), that the spontaneous emission rate associated
with an electric quarrupole transition is
Here,
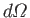 is the solid angle associated with the
direction of the
emitted photon's normalized wavevector,
is the solid angle associated with the
direction of the
emitted photon's normalized wavevector, 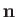 . Moreover,
. Moreover,

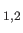 are the photon's two independent electric polarization vectors.
are the photon's two independent electric polarization vectors.
The selection rules for electric quadrupole transitions in a hydrogen-like atom are [23]
where  is the azimuthal quantum number,
is the azimuthal quantum number,  the magnetic quantum number, and
the magnetic quantum number, and 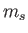 the spin quantum
number.
A more general form of these selection rules is
the spin quantum
number.
A more general form of these selection rules is
where 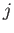 and
and 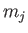 are the standard quantum numbers associated with the total angular
momentum of the system. Note, however, that electric
quadrupole transitions between two
are the standard quantum numbers associated with the total angular
momentum of the system. Note, however, that electric
quadrupole transitions between two 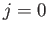 states, or between two
states, or between two 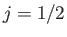 states, or
between a
states, or
between a 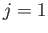 state and a
state and a 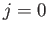 state, are forbidden [23].
state, are forbidden [23].
Let us estimate the typical spontaneous emission rate for an electric quadrupole transition in a hydrogen atom.
We expect the matrix element
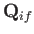 , defined in Equation (8.216), to be of order
, defined in Equation (8.216), to be of order 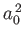 ,
where
,
where 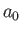 is the Bohr radius.
We also expect
is the Bohr radius.
We also expect
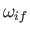 to be of order
to be of order
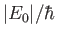 , where
, where 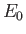 is the hydrogen ground-state energy.
It thus follows from Equation (8.217) that
is the hydrogen ground-state energy.
It thus follows from Equation (8.217) that
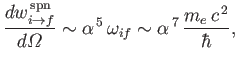 |
(8.220) |
which is of order
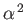 times smaller than a typical electric dipole transition rate. [See Equations (8.180).]
times smaller than a typical electric dipole transition rate. [See Equations (8.180).]



Next: Photo-Ionization
Up: Time-Dependent Perturbation Theory
Previous: Magnetic Dipole Transitions
Richard Fitzpatrick
2016-01-22
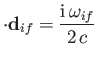
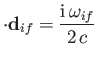
![]() , defined in Equation (8.216), to be of order
, defined in Equation (8.216), to be of order ![]() ,
where
,
where ![]() is the Bohr radius.
We also expect
is the Bohr radius.
We also expect
![]() to be of order
to be of order
![]() , where
, where ![]() is the hydrogen ground-state energy.
It thus follows from Equation (8.217) that
is the hydrogen ground-state energy.
It thus follows from Equation (8.217) that