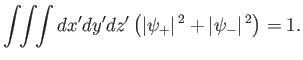Next: Rotation Operators in Spin
Up: Spin Angular Momentum
Previous: Properties of Spin Angular
Wavefunction of Spin One-Half Particle
The state of a spin one-half particle is represented as a vector in ket space.
Let us suppose that this space is spanned by the basis kets
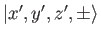 . Here,
. Here,
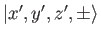 denotes a
simultaneous eigenstate of the position operators
denotes a
simultaneous eigenstate of the position operators  ,
, 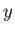 ,
, 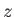 , and
the spin operator
, and
the spin operator 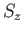 , corresponding to the eigenvalues
, corresponding to the eigenvalues 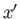 ,
, 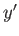 ,
, 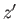 ,
and
,
and
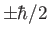 , respectively. The basis kets are assumed to
satisfy the completeness relation
, respectively. The basis kets are assumed to
satisfy the completeness relation
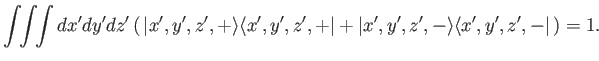 |
(5.15) |
It is helpful to think of the ket
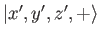 as the product
of two kets--a position-space ket
as the product
of two kets--a position-space ket
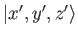 , and
a spin-space ket
, and
a spin-space ket 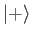 . We assume that such a product obeys
the commutative and distributive axioms of multiplication:
. We assume that such a product obeys
the commutative and distributive axioms of multiplication:
where the 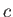 's are numbers. We can give meaning to any
position space operator (such as
's are numbers. We can give meaning to any
position space operator (such as 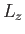 ) acting on the product
) acting on the product
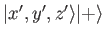 by assuming that it operates only on the
by assuming that it operates only on the
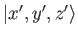 factor, and commutes with the
factor, and commutes with the 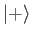 factor.
Similarly, we can give a meaning to any spin operator (such as
factor.
Similarly, we can give a meaning to any spin operator (such as 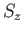 ) acting
on
) acting
on
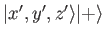 by assuming that it operates only on
by assuming that it operates only on 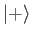 , and
commutes with
, and
commutes with
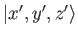 . This implies that every position
space operator
commutes with every spin operator. In this manner, we can give
a meaning to the equation
. This implies that every position
space operator
commutes with every spin operator. In this manner, we can give
a meaning to the equation
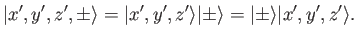 |
(5.19) |
The multiplication in the previous equation is of a quite different type to
any that we have encountered previously. The ket vectors
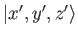 and
and
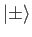 lie in two completely separate vector spaces, and their product
lie in two completely separate vector spaces, and their product
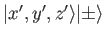 lies in a third vector space.
In mathematics, the latter space
is termed the product space of the former spaces, which are
termed factor spaces. The dimensionality a product space is equal to the product of the dimensionalities
of each of the factor spaces. Actually, a general ket in the product space is not
of the form (5.19), but is instead a sum, or integral, of kets of this form.
lies in a third vector space.
In mathematics, the latter space
is termed the product space of the former spaces, which are
termed factor spaces. The dimensionality a product space is equal to the product of the dimensionalities
of each of the factor spaces. Actually, a general ket in the product space is not
of the form (5.19), but is instead a sum, or integral, of kets of this form.
A general state, 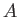 , of a spin one-half particle is represented as a ket,
, of a spin one-half particle is represented as a ket,
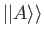 , in the product of the spin and position spaces.
This state can be completely specified by two wavefunctions:
, in the product of the spin and position spaces.
This state can be completely specified by two wavefunctions:
The probability of observing the particle in the region 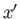 to
to 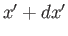 ,
,
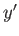 to
to 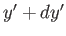 , and
, and 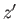 to
to 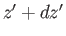 , with
, with
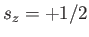 , is
, is
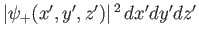 . Likewise,
the probability of observing the particle in the region
. Likewise,
the probability of observing the particle in the region 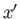 to
to 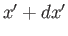 ,
,
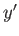 to
to 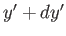 , and
, and 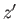 to
to 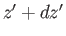 , with
, with
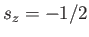 , is
, is
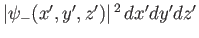 .
The normalization condition for the wavefunctions is
.
The normalization condition for the wavefunctions is
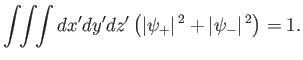 |
(5.22) |



Next: Rotation Operators in Spin
Up: Spin Angular Momentum
Previous: Properties of Spin Angular
Richard Fitzpatrick
2016-01-22
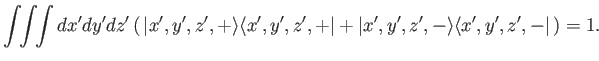
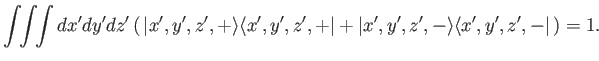
![]() as the product
of two kets--a position-space ket
as the product
of two kets--a position-space ket
![]() , and
a spin-space ket
, and
a spin-space ket ![]() . We assume that such a product obeys
the commutative and distributive axioms of multiplication:
. We assume that such a product obeys
the commutative and distributive axioms of multiplication:
![]() and
and
![]() lie in two completely separate vector spaces, and their product
lie in two completely separate vector spaces, and their product
![]() lies in a third vector space.
In mathematics, the latter space
is termed the product space of the former spaces, which are
termed factor spaces. The dimensionality a product space is equal to the product of the dimensionalities
of each of the factor spaces. Actually, a general ket in the product space is not
of the form (5.19), but is instead a sum, or integral, of kets of this form.
lies in a third vector space.
In mathematics, the latter space
is termed the product space of the former spaces, which are
termed factor spaces. The dimensionality a product space is equal to the product of the dimensionalities
of each of the factor spaces. Actually, a general ket in the product space is not
of the form (5.19), but is instead a sum, or integral, of kets of this form.
![]() , of a spin one-half particle is represented as a ket,
, of a spin one-half particle is represented as a ket,
![]() , in the product of the spin and position spaces.
This state can be completely specified by two wavefunctions:
, in the product of the spin and position spaces.
This state can be completely specified by two wavefunctions: