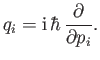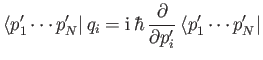Next: Heisenberg Uncertainty Principle
Up: Position and Momentum
Previous: Generalized Schrödinger Representation
Momentum Representation
Consider a system with one degree of freedom, describable in terms of a coordinate
 and its conjugate momentum
and its conjugate momentum 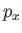 , both of which have a continuous range of
eigenvalues. We have seen that it is possible to represent the system in terms
of the eigenkets of
, both of which have a continuous range of
eigenvalues. We have seen that it is possible to represent the system in terms
of the eigenkets of  .
This is termed the Schrödinger representation.
However, it is also possible to represent the system in
terms of the eigenkets of
.
This is termed the Schrödinger representation.
However, it is also possible to represent the system in
terms of the eigenkets of 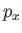 .
.
Consider the eigenkets of 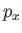 that belong to the eigenvalues
that belong to the eigenvalues 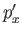 . These are
denoted
. These are
denoted
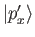 . The orthogonality relation for the momentum eigenkets is
. The orthogonality relation for the momentum eigenkets is
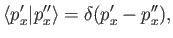 |
(2.80) |
and the corresponding completeness relation is
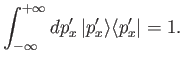 |
(2.81) |
A general state ket can be written
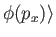 |
(2.82) |
where the standard ket 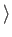 satisfies
satisfies
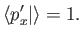 |
(2.83) |
Note that the standard ket in this representation is quite
different to that in the Schrödinger representation.
The momentum space wavefunction
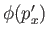 satisfies
satisfies
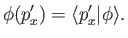 |
(2.84) |
The probability that a measurement of the momentum yields a result
lying in the range 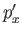 to
to
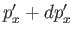 is given by
is given by
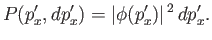 |
(2.85) |
Finally, the normalization condition for a physical momentum space wavefunction is
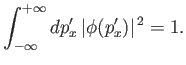 |
(2.86) |
The fundamental commutation relations (2.23)-(2.25) exhibit a
particular symmetry between coordinates and their conjugate momenta. In fact, if all the
coordinates are transformed into their conjugate momenta, and vice versa, and
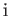 is then replaced by
is then replaced by 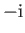 , then the commutation relations are
unchanged. It follows from this symmetry that we can always choose the eigenkets
of
, then the commutation relations are
unchanged. It follows from this symmetry that we can always choose the eigenkets
of 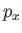 in such a manner that the coordinate
in such a manner that the coordinate
 can be represented as
can be represented as
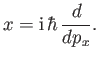 |
(2.87) |
(See Section 2.4.)
This scheme is termed the momentum representation.
The previous result is easily generalized to a system with more than one degree of
freedom. Suppose the system is specified by 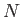 coordinates,
coordinates,
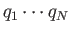 , and
, and
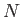 conjugate momenta,
conjugate momenta,
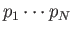 . Then, in the momentum representation, the
coordinates can be written as
. Then, in the momentum representation, the
coordinates can be written as
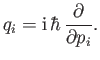 |
(2.88) |
We also have
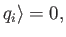 |
(2.89) |
and
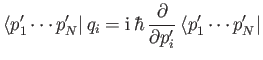 |
(2.90) |
[cf., Equation (2.78).]
Generally speaking, the momentum representation is less useful than the Schrödinger representation. The
main reason for this is that the energy operators (i.e., the Hamiltonians) of
most simple microscopic systems take the form of a sum of quadratic terms in the momenta
(i.e., the kinetic energy) plus a complicated function of the coordinates
(i.e., the potential energy). In the Schrödinger representation,
the eigenvalue problem for the energy translates into a second-order partial differential
equation in the coordinates, with a complicated potential function. In the
momentum representation, the problem transforms into a high-order partial differential
equation in the momenta, with a quadratic potential. With the mathematical
tools at our disposal, we are far better able to solve the former type of differential equation
than the latter.



Next: Heisenberg Uncertainty Principle
Up: Position and Momentum
Previous: Generalized Schrödinger Representation
Richard Fitzpatrick
2016-01-22
![]() that belong to the eigenvalues
that belong to the eigenvalues ![]() . These are
denoted
. These are
denoted
![]() . The orthogonality relation for the momentum eigenkets is
. The orthogonality relation for the momentum eigenkets is
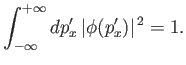
![]() is then replaced by
is then replaced by ![]() , then the commutation relations are
unchanged. It follows from this symmetry that we can always choose the eigenkets
of
, then the commutation relations are
unchanged. It follows from this symmetry that we can always choose the eigenkets
of ![]() in such a manner that the coordinate
in such a manner that the coordinate
![]() can be represented as
can be represented as
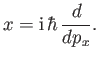
![]() coordinates,
coordinates,
![]() , and
, and
![]() conjugate momenta,
conjugate momenta,
![]() . Then, in the momentum representation, the
coordinates can be written as
. Then, in the momentum representation, the
coordinates can be written as