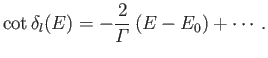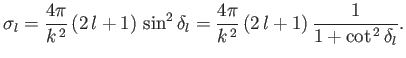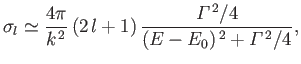Next: Elastic and Inelastic Scattering
Up: Scattering Theory
Previous: Low-Energy Scattering
There is a significant exception to the energy independence of the scattering cross-section at low
incident energies described in the previous section. Suppose that the quantity
 is slightly less than
is slightly less than  . As the incident energy increases,
. As the incident energy increases, 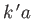 ,
which is given by Equation (10.129), can reach the value
,
which is given by Equation (10.129), can reach the value  . In this case,
. In this case,
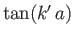 becomes infinite, so we can no longer assume that the right-hand side of Equation (10.124) is small. In fact,
at the value of the incident energy
at which
becomes infinite, so we can no longer assume that the right-hand side of Equation (10.124) is small. In fact,
at the value of the incident energy
at which
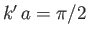 , it follows from Equation (10.124) that
, it follows from Equation (10.124) that
 ,
or
,
or
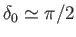 (because we are assuming that
(because we are assuming that  ).
This implies that
).
This implies that
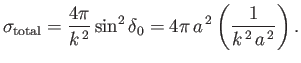 |
(10.130) |
Note that the total scattering cross-section now depends on the energy. Furthermore, the
magnitude of the cross-section is much larger than that given in Equation (10.128)
for
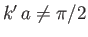 (because
(because  , whereas
, whereas
 ).
).
The origin of the rather strange behavior described in the previous paragraph is easily explained. The condition
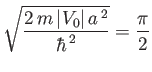 |
(10.131) |
is equivalent to the condition that a spherical well of depth
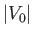 possesses a bound state at zero energy. Thus, for a potential
well that satisfies the preceding equation, the energy of the scattering system
is essentially the same as the energy of the bound state. In this situation,
an incident particle would like to form a bound state in the potential
well. However, the bound state is not stable, because the system has a small
positive energy. Nevertheless, this sort of resonant scattering
is best understood as the capture of an incident particle to form
a metastable bound state, followed by the decay of the bound state
and release of the particle. The cross-section for resonant scattering
is generally far higher than that for non-resonant scattering.
possesses a bound state at zero energy. Thus, for a potential
well that satisfies the preceding equation, the energy of the scattering system
is essentially the same as the energy of the bound state. In this situation,
an incident particle would like to form a bound state in the potential
well. However, the bound state is not stable, because the system has a small
positive energy. Nevertheless, this sort of resonant scattering
is best understood as the capture of an incident particle to form
a metastable bound state, followed by the decay of the bound state
and release of the particle. The cross-section for resonant scattering
is generally far higher than that for non-resonant scattering.
We have seen that there is a resonant effect when the phase-shift of
the S-wave takes the value  . There is nothing special about
the
. There is nothing special about
the  partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the
partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the  th partial
wave is
th partial
wave is  . Suppose that
. Suppose that 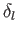 attains the value
attains the value
 at the incident energy
at the incident energy 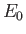 , so that
, so that
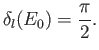 |
(10.132) |
Let us expand
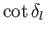 in the vicinity of the resonant energy:
in the vicinity of the resonant energy:
Defining
![$\displaystyle \left[\frac{d \delta_l(E)}{d E} \right]_{E=E_0} = \frac{2}{{\mit\Gamma}},$](img3675.png) |
(10.134) |
we obtain
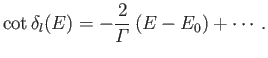 |
(10.135) |
Recall, from Equation (10.93), that the contribution of the  th partial wave
to the total scattering cross-section is
th partial wave
to the total scattering cross-section is
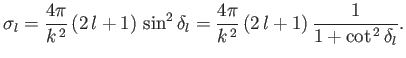 |
(10.136) |
Thus,
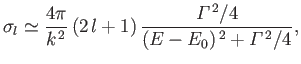 |
(10.137) |
which is known as the Breit-Wigner formula [16]. The variation of
the partial cross-section, 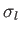 , with the incident energy has
the form of a classical resonance curve. The quantity
, with the incident energy has
the form of a classical resonance curve. The quantity
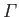 is
the width of the resonance (in energy). We can interpret the
Breit-Wigner formula as describing the absorption of an incident particle
to form a metastable state, of energy
is
the width of the resonance (in energy). We can interpret the
Breit-Wigner formula as describing the absorption of an incident particle
to form a metastable state, of energy 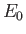 , and lifetime
, and lifetime
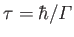 .
.



Next: Elastic and Inelastic Scattering
Up: Scattering Theory
Previous: Low-Energy Scattering
Richard Fitzpatrick
2016-01-22
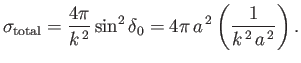
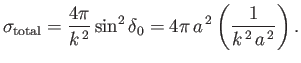
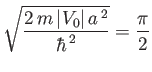
![]() . There is nothing special about
the
. There is nothing special about
the ![]() partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the
partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the ![]() th partial
wave is
th partial
wave is ![]() . Suppose that
. Suppose that ![]() attains the value
attains the value
![]() at the incident energy
at the incident energy ![]() , so that
, so that
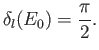
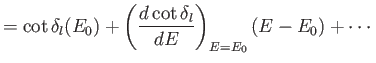
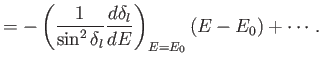
![$\displaystyle \left[\frac{d \delta_l(E)}{d E} \right]_{E=E_0} = \frac{2}{{\mit\Gamma}},$](img3675.png)