Next: Bibliography Up: Rotation Braking in Tokamak Previous: Rotation Braking by a Contents
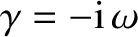 . This observation leads us
to formulate the following generalization of the torque balance model presented in the
Section 10.2:
. This observation leads us
to formulate the following generalization of the torque balance model presented in the
Section 10.2:
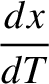 |
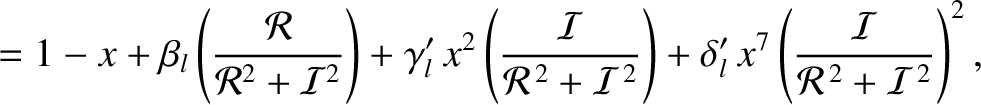 |
(10.113) |
 |
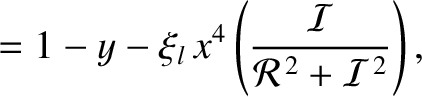 |
(10.114) |
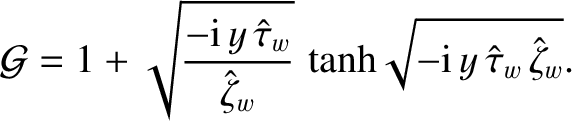 |
(10.115) |
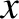 is the width of the magnetic island chain relative to its saturated width when the wall is perfectly conducting,
is the width of the magnetic island chain relative to its saturated width when the wall is perfectly conducting, 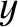 is the island
rotation frequency relative to its value when there is no interaction with the wall, and
is the island
rotation frequency relative to its value when there is no interaction with the wall, and 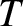 is time
normalized to the typical time required for the island chain to attain is final saturated width.
Moreover,
is time
normalized to the typical time required for the island chain to attain is final saturated width.
Moreover, 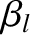 ,
, 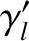 ,
, 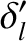 ,
,  ,
, 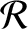 ,
, 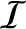 ,
,
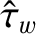 , and
, and
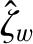 are defined in Equations (10.20), (10.102), (10.103), (10.110), (10.91), (10.92), (10.98),
and (10.101), respectively. The improved torque balance model should be capable of accurately predicting the critical island
width that must be exceeded in order to trigger a collapse in the island rotation frequency, even when the thin-wall approximation breaks down, despite not being able to
accurately predict the timescale on which the rotation collapse occurs.
are defined in Equations (10.20), (10.102), (10.103), (10.110), (10.91), (10.92), (10.98),
and (10.101), respectively. The improved torque balance model should be capable of accurately predicting the critical island
width that must be exceeded in order to trigger a collapse in the island rotation frequency, even when the thin-wall approximation breaks down, despite not being able to
accurately predict the timescale on which the rotation collapse occurs.
![\includegraphics[width=\textwidth]{Chapter10/Figure10_9.eps}](img3347.png)
|
Figure 10.9 shows the critical island width required to trigger a rotation collapse calculated as a
function of the wall thickness, for various different unperturbed island rotation frequencies, using the improved torque balance model. Separate calculations are made for a low-field and a high-field tokamak
fusion reactor. (See Chapter 1.) The calculation parameters are determined using the following assumptions:
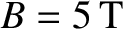 (low-field) or
(low-field) or
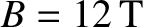 (high-field),
(high-field),
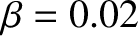 ,
,
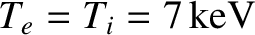 ,
,
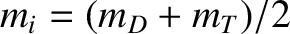 (where
(where 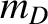 and
and 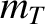 are the deuteron and triton masses, respectively),
are the deuteron and triton masses, respectively),
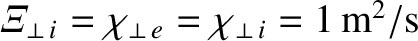 ,
, 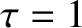 ,
,
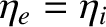 , and
, and
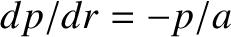 . The plasma equilibrium is
assumed to be of the Wesson type (see Section 9.4), with
. The plasma equilibrium is
assumed to be of the Wesson type (see Section 9.4), with 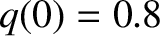 and
and 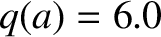 .
The poloidal and toroidal mode numbers of the tearing mode are
.
The poloidal and toroidal mode numbers of the tearing mode are 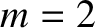 and
and  , respectively. It follows that
, respectively. It follows that
 . The perfect-wall saturated
island width is
. The perfect-wall saturated
island width is
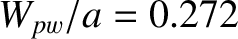 . The wall radius and resistivity are assumed to be
. The wall radius and resistivity are assumed to be
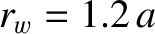 and
and
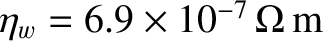 (which is the electrical resistivity of stainless steel), respectively.
(which is the electrical resistivity of stainless steel), respectively.
As is clear from Figure 10.9, the critical island width required to trigger rotation collapse
increases with increasing wall thickness (because the wall becomes less electrically resistive) until
a critical thickness is reached above which the critical island width becomes independent of the wall
thickness. Of course, the critical wall thickness is that above which the thin-wall approximation breaks down. The eddy current
induced by the rotating island chain in a wall whose thickness is greater than the critical thickness (which corresponds to
a skin-depth in the wall material) only penetrates a skin-depth into the wall from its inner boundary, which
implies that the effective thickness of the wall becomes the skin-depth, rather than its actual thickness.
According to the figure, for a plasma with diamagnetic levels of ion fluid rotation (i.e.,
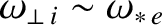 ), the critical island width is below 10% of the plasma minor radius for thin (i.e.,
), the critical island width is below 10% of the plasma minor radius for thin (i.e.,
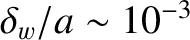 ) resistive walls. On the other hand, the critical island width is about twice this value for thick (i.e.,
) resistive walls. On the other hand, the critical island width is about twice this value for thick (i.e.,
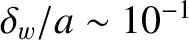 )
conducting walls. As before, it is apparent that a low-field tokamak fusion reactor is more susceptible to rotation braking than a high-field
fusion reactor because of its lower diamagnetic frequency, and consequent lower ion fluid rotation.
)
conducting walls. As before, it is apparent that a low-field tokamak fusion reactor is more susceptible to rotation braking than a high-field
fusion reactor because of its lower diamagnetic frequency, and consequent lower ion fluid rotation.