Rutherford Scattering Cross-Section
Consider a species-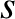 particle, incident with relative velocity
particle, incident with relative velocity 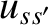 onto an ensemble of species-
onto an ensemble of species-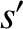 particles with number density
particles with number density 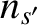 .
If
.
If
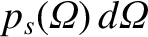 is the probability per unit time of the particle being scattered into the range of solid angle
is the probability per unit time of the particle being scattered into the range of solid angle
 to
to
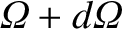 then the differential scattering cross-section,
then the differential scattering cross-section,
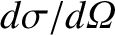 , is defined via (Reif 1965)
, is defined via (Reif 1965)
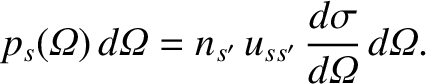 |
(3.65) |
Assuming that the scattering is azimuthally symmetric (i.e., symmetric in 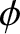 ), we can
write
), we can
write
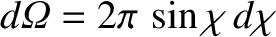 . Now, the probability per unit time of a collision having an impact parameter in the range
. Now, the probability per unit time of a collision having an impact parameter in the range
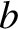 to
to 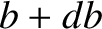 is
is
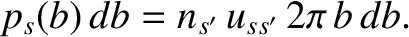 |
(3.66) |
Furthermore, we can write
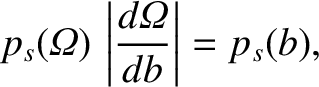 |
(3.67) |
provided that 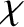 and
and 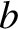 are related according to the two-particle scattering law, Equation (3.64).
(The absolute value of
are related according to the two-particle scattering law, Equation (3.64).
(The absolute value of
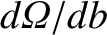 is taken because
is taken because 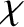 is a monotonically decreasing function of
is a monotonically decreasing function of 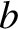 .)
It follows that
.)
It follows that
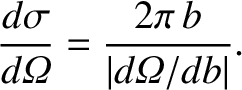 |
(3.68) |
Equation (3.64) yields
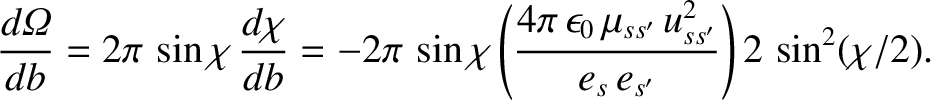 |
(3.69) |
Finally, Equations (3.64), (3.68), and (3.69) can be combined to give the so-called
Rutherford scattering cross-section,
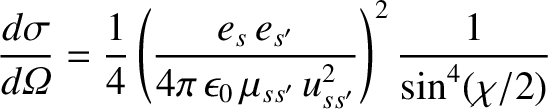 |
(3.70) |
(Rutherford 1911).
It is immediately apparent, from the previous formula, that two-particle Coulomb collisions are dominated by
small-angle (i.e., small 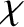 ) scattering events.
) scattering events.
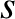 particle, incident with relative velocity
particle, incident with relative velocity 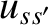 onto an ensemble of species-
onto an ensemble of species-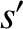 particles with number density
particles with number density 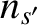 .
If
.
If
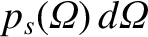 is the probability per unit time of the particle being scattered into the range of solid angle
is the probability per unit time of the particle being scattered into the range of solid angle
 to
to
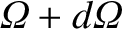 then the differential scattering cross-section,
then the differential scattering cross-section,
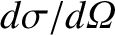 , is defined via (Reif 1965)
, is defined via (Reif 1965)
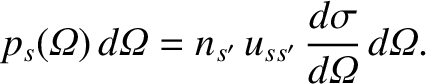
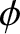 ), we can
write
), we can
write
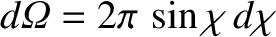 . Now, the probability per unit time of a collision having an impact parameter in the range
. Now, the probability per unit time of a collision having an impact parameter in the range
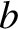 to
to 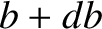 is
is
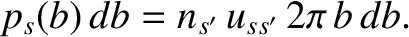
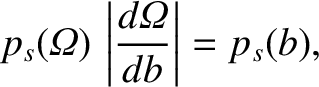
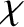 and
and 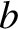 are related according to the two-particle scattering law, Equation (3.64).
(The absolute value of
are related according to the two-particle scattering law, Equation (3.64).
(The absolute value of
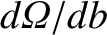 is taken because
is taken because 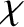 is a monotonically decreasing function of
is a monotonically decreasing function of 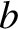 .)
It follows that
Equation (3.64) yields
Finally, Equations (3.64), (3.68), and (3.69) can be combined to give the so-called
Rutherford scattering cross-section,
(Rutherford 1911).
It is immediately apparent, from the previous formula, that two-particle Coulomb collisions are dominated by
small-angle (i.e., small
.)
It follows that
Equation (3.64) yields
Finally, Equations (3.64), (3.68), and (3.69) can be combined to give the so-called
Rutherford scattering cross-section,
(Rutherford 1911).
It is immediately apparent, from the previous formula, that two-particle Coulomb collisions are dominated by
small-angle (i.e., small 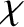 ) scattering events.
) scattering events.