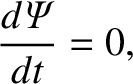Flux Freezing
The MHD Ohm's law,
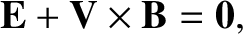 |
(8.13) |
is sometimes referred to as the perfect conductivity equation (for
obvious reasons), and sometimes as the flux freezing equation.
The latter nomenclature comes about because Equation (8.13) implies that the magnetic
flux through any loop in the plasma, each element of
which moves with the local plasma velocity, is a conserved quantity.
In order to verify the previous assertion, let us consider the
magnetic flux,
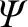 , through a loop,
, through a loop,  , that is co-moving
with the plasma:
, that is co-moving
with the plasma:
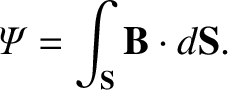 |
(8.14) |
Here, 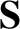 is some surface that spans
is some surface that spans  . The time rate of
change of
. The time rate of
change of
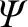 is made up of two parts. First, there
is the part due to the time variation of
is made up of two parts. First, there
is the part due to the time variation of 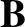 over the
surface
over the
surface 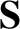 , which can be written
, which can be written
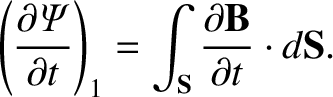 |
(8.15) |
Using the Faraday-Maxwell equation, this reduces to
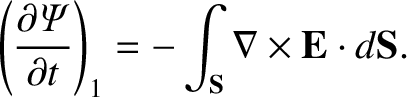 |
(8.16) |
Second, there is the part due to the motion of  . If
. If 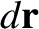 is an element of
is an element of  then
then
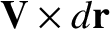 is the area swept out
by
is the area swept out
by 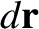 per unit time. Hence, the flux crossing this area is
per unit time. Hence, the flux crossing this area is
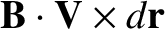 .
It follows that
.
It follows that
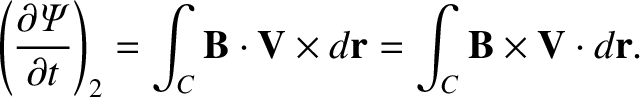 |
(8.17) |
Using the curl theorem, we obtain
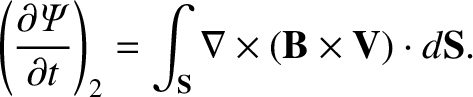 |
(8.18) |
Hence, the total time rate of change of
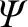 is given by
is given by
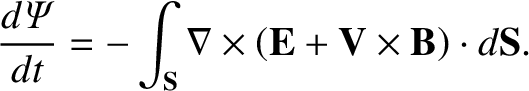 |
(8.19) |
The condition
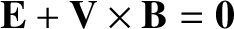 |
(8.20) |
clearly implies that
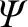 remains constant in time
for any arbitrary co-moving loop,
remains constant in time
for any arbitrary co-moving loop,  .
This, in turn, implies that magnetic field-lines must move with the
plasma. In other words, the field-lines are frozen into the plasma.
.
This, in turn, implies that magnetic field-lines must move with the
plasma. In other words, the field-lines are frozen into the plasma.
A flux-tube is defined as a topologically cylindrical volume whose
sides are defined by magnetic field-lines. Suppose that, at some initial
time, a flux-tube is embedded in the plasma. According to the flux-freezing
constraint,
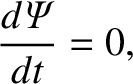 |
(8.21) |
the subsequent motion of the plasma and the magnetic field is always
such that it maintains the integrity of the flux-tube. Because magnetic
field-lines can be regarded as infinitely thin flux-tubes, we conclude that
MHD plasma motion also maintains the integrity of field-lines. In other words,
magnetic field-lines embedded in an MHD plasma can never break and reconnect:
that is, MHD forbids any change in topology of the field-lines. It turns
out that this is an extremely restrictive constraint. We shall discuss
situations in which this constraint is relaxed in Chapter 9.
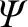 , through a loop,
, through a loop,  , that is co-moving
with the plasma:
, that is co-moving
with the plasma:
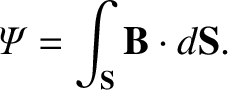
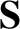 is some surface that spans
is some surface that spans  . The time rate of
change of
. The time rate of
change of
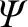 is made up of two parts. First, there
is the part due to the time variation of
is made up of two parts. First, there
is the part due to the time variation of 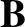 over the
surface
over the
surface 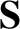 , which can be written
, which can be written
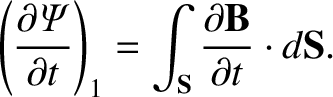
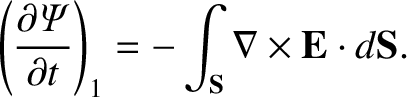
 . If
. If 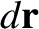 is an element of
is an element of  then
then
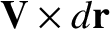 is the area swept out
by
is the area swept out
by 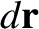 per unit time. Hence, the flux crossing this area is
per unit time. Hence, the flux crossing this area is
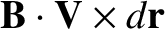 .
It follows that
.
It follows that
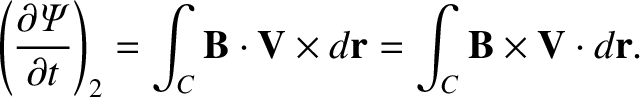
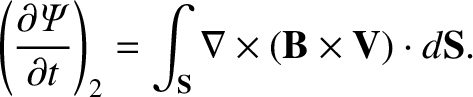
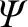 is given by
is given by
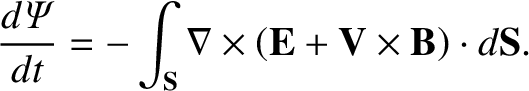
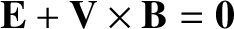
 remains constant in time
for any arbitrary co-moving loop,
remains constant in time
for any arbitrary co-moving loop,  .
This, in turn, implies that magnetic field-lines must move with the
plasma. In other words, the field-lines are frozen into the plasma.
.
This, in turn, implies that magnetic field-lines must move with the
plasma. In other words, the field-lines are frozen into the plasma.