Harris Instability
It is not feasible to give a comprehensive account of velocity-space instabilities in a magnetized plasma, on account of the
great number of different instabilities of this type. Rather than trying to analyze the full electromagnetic dispersion relation,
we shall concentrate on the stability of electrostatic waves. Instabilities of this type
tend to be more important than electromagnetic instabilities, particularly in low-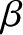 plasmas (Cairns 1985). Our starting point is the
Harris dispersion relation, (7.119):
Making use of the Plemelj formula, (7.26), we can write the previous expression in the form
plasmas (Cairns 1985). Our starting point is the
Harris dispersion relation, (7.119):
Making use of the Plemelj formula, (7.26), we can write the previous expression in the form
 |
(7.153) |
where
 |
(7.154) |
and
Generally speaking, we expect
 . Let us search for an instability whose angular frequency is
. Let us search for an instability whose angular frequency is
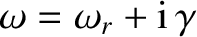 , where
, where 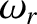 is real and positive,
is real and positive, 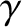 is real, and
is real, and
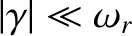 .
Thus,
.
Thus, 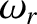 is the real frequency of the instability,
is the real frequency of the instability,
 its phase-velocity, and
its phase-velocity, and 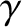 its growth-rate.
Expanding (7.153) to first-order in
its growth-rate.
Expanding (7.153) to first-order in 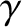 , we obtain
, we obtain
 |
(7.156) |
Here, the quantities
 ,
,
 , and
, and
 are all real.
Thus, the real frequency of the instability is determined from
are all real.
Thus, the real frequency of the instability is determined from
 |
(7.157) |
whereas the growth-rate is given by
 |
(7.158) |
Consider the so-called Harris instability, which occurs for real frequencies close to the ion cyclotron harmonics in a
plasma in which the parallel and perpendicular (to the equilibrium magnetic field) temperatures are different (Harris 1970; Cairns 1985).
Suppose that the equilibrium velocity distribution functions are two-temperature Maxwellians of the form
 |
(7.159) |
Here,
 and
and
 are the species-
are the species-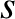 perpendicular and parallel temperatures, respectively.
It follows that
and
where
perpendicular and parallel temperatures, respectively.
It follows that
and
where
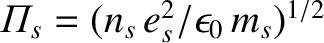 ,
,
 , and
, and
 .
Moreover,
.
Moreover,  and
and
 denote the principal part and the remainder of the plasma dispersion function, respectively.
However, according to Section 7.4,
Hence, we can write
denote the principal part and the remainder of the plasma dispersion function, respectively.
However, according to Section 7.4,
Hence, we can write
Suppose, for the sake of simplicity, that the electrons are “cold” but the ions are “hot.” In other words,
 for the
electrons, but not for the ions. In this situation, Equation (7.160) reduces to
for the
electrons, but not for the ions. In this situation, Equation (7.160) reduces to
 |
(7.165) |
The ion contribution to the previous expression is negligible compared to the electron contribution, because of the  dependence of
dependence of
 .
The real frequency of the instability is determined from
.
The real frequency of the instability is determined from
 |
(7.166) |
which implies that
 |
(7.167) |
Furthermore,
 |
(7.168) |
Hence, the growth-rate of the instability is written
 |
(7.169) |
or
The electron contribution to the previous expression is negligible compared to the ion contribution, because
 .
.
Figure 7.11:
Schematic diagram showing the growth-rate of the Harris instability as a function of its real frequency.
|
|
It can be seen, from the previous formula, that if
 then
then  for all values of
for all values of 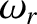 (recall that
(recall that
 ). In other words, there
is no instability if the perpendicular and parallel ion temperatures are equal to one another. On the other hand, if
). In other words, there
is no instability if the perpendicular and parallel ion temperatures are equal to one another. On the other hand, if
 then there is a range of
then there is a range of 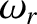 values for which each term in the sum on the right-hand
side of (7.170) is positive. In other words, there is the possibility of an instability.
The variation of
values for which each term in the sum on the right-hand
side of (7.170) is positive. In other words, there is the possibility of an instability.
The variation of
 with
with 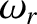 is shown schematically in Figure 7.11 for a
case where
is shown schematically in Figure 7.11 for a
case where
 is relatively large. It can be seen that the
growth-rate is positive in a narrow range of real frequencies lying on the low frequency side of each harmonic
of the ion cyclotron frequency, and negative in a similar range of frequencies on the high frequency side.
is relatively large. It can be seen that the
growth-rate is positive in a narrow range of real frequencies lying on the low frequency side of each harmonic
of the ion cyclotron frequency, and negative in a similar range of frequencies on the high frequency side.
According to Equation (7.167), 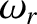 varies from zero to
varies from zero to
 . Thus, a necessary condition for
obtaining an instability close to the
. Thus, a necessary condition for
obtaining an instability close to the 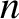 th ion cyclotron harmonic is
th ion cyclotron harmonic is
 . Now,
the positive contribution from the
. Now,
the positive contribution from the 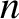 th term in the sum on the right-hand side of Equation (7.170) peaks close to
th term in the sum on the right-hand side of Equation (7.170) peaks close to
 |
(7.171) |
In order for the net growth-rate to be positive, we require that
 |
(7.172) |
which implies that (Harris 1970)
 |
(7.173) |
If this inequality is not satisfied then the negative contribution from the  th term in the sum predominates over the
positive contribution from the
th term in the sum predominates over the
positive contribution from the 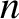 th term. Observe that the previous inequality becomes harder to satisfy as
th term. Observe that the previous inequality becomes harder to satisfy as 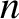 increases.
increases.
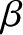 plasmas (Cairns 1985). Our starting point is the
Harris dispersion relation, (7.119):
plasmas (Cairns 1985). Our starting point is the
Harris dispersion relation, (7.119):


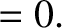
 . Let us search for an instability whose angular frequency is
. Let us search for an instability whose angular frequency is
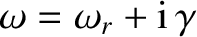 , where
, where 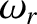 is real and positive,
is real and positive, 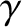 is real, and
is real, and
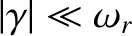 .
Thus,
.
Thus, 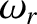 is the real frequency of the instability,
is the real frequency of the instability,
 its phase-velocity, and
its phase-velocity, and 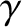 its growth-rate.
Expanding (7.153) to first-order in
its growth-rate.
Expanding (7.153) to first-order in 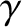 , we obtain
, we obtain

 ,
,
 , and
, and
 are all real.
Thus, the real frequency of the instability is determined from
are all real.
Thus, the real frequency of the instability is determined from


 and
and
 are the species-
are the species-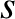 perpendicular and parallel temperatures, respectively.
It follows that
and
where
perpendicular and parallel temperatures, respectively.
It follows that
and
where
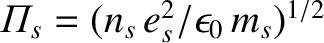 ,
,
 , and
, and
 .
Moreover,
.
Moreover,  and
and
 denote the principal part and the remainder of the plasma dispersion function, respectively.
However, according to Section 7.4,
denote the principal part and the remainder of the plasma dispersion function, respectively.
However, according to Section 7.4,






![$\displaystyle \phantom{=} \times\left[\frac{n\,{\mit\Omega}_s}{k_\parallel\,v_{...
...\frac{\omega-n\,{\mit\Omega}_s}{k_\parallel\,v_{\parallel\,s}}\right)^2\right].$](img2625.png)
 for the
electrons, but not for the ions. In this situation, Equation (7.160) reduces to
for the
electrons, but not for the ions. In this situation, Equation (7.160) reduces to

 dependence of
dependence of
 .
The real frequency of the instability is determined from
.
The real frequency of the instability is determined from



 .
.
![\includegraphics[height=2.75in]{Chapter07/fig7_11.eps}](img2638.png)
 then
then  for all values of
for all values of 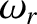 (recall that
(recall that
 ). In other words, there
is no instability if the perpendicular and parallel ion temperatures are equal to one another. On the other hand, if
). In other words, there
is no instability if the perpendicular and parallel ion temperatures are equal to one another. On the other hand, if
 then there is a range of
then there is a range of 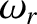 values for which each term in the sum on the right-hand
side of (7.170) is positive. In other words, there is the possibility of an instability.
The variation of
values for which each term in the sum on the right-hand
side of (7.170) is positive. In other words, there is the possibility of an instability.
The variation of
 with
with 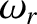 is shown schematically in Figure 7.11 for a
case where
is shown schematically in Figure 7.11 for a
case where
 is relatively large. It can be seen that the
growth-rate is positive in a narrow range of real frequencies lying on the low frequency side of each harmonic
of the ion cyclotron frequency, and negative in a similar range of frequencies on the high frequency side.
is relatively large. It can be seen that the
growth-rate is positive in a narrow range of real frequencies lying on the low frequency side of each harmonic
of the ion cyclotron frequency, and negative in a similar range of frequencies on the high frequency side.
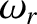 varies from zero to
varies from zero to
 . Thus, a necessary condition for
obtaining an instability close to the
. Thus, a necessary condition for
obtaining an instability close to the 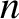 th ion cyclotron harmonic is
th ion cyclotron harmonic is
 . Now,
the positive contribution from the
. Now,
the positive contribution from the 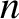 th term in the sum on the right-hand side of Equation (7.170) peaks close to
th term in the sum on the right-hand side of Equation (7.170) peaks close to



 th term in the sum predominates over the
positive contribution from the
th term in the sum predominates over the
positive contribution from the 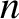 th term. Observe that the previous inequality becomes harder to satisfy as
th term. Observe that the previous inequality becomes harder to satisfy as 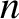 increases.
increases.