Current-Driven Ion Acoustic Instability
As a second example, consider ion acoustic waves in a plasma with single-charged ions in which the electron velocity distribution function takes the simplified form
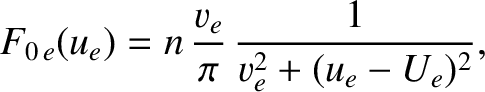 |
(7.134) |
and the ion distribution is written
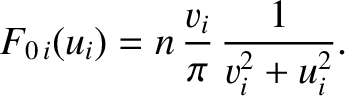 |
(7.135) |
Here, 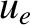 and
and 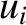 are the parallel (to
are the parallel (to 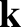 ) electron and ion velocities, respectively,
) electron and ion velocities, respectively, 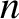 is the particle number density,
is the particle number density,
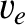 and
and 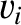 are the electron and ion thermal spreads, respectively, and
are the electron and ion thermal spreads, respectively, and 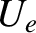 is the electron-ion drift velocity. We saw in Section 7.5 that,
in the absence of drift, the ion acoustic wave is damped. We now wish to investigate whether the presence of an electron-ion drift (which is associated with
a net current flowing in the plasma) can destabilize the mode. The appropriate dispersion relation is Equation (7.49), which, on
integration by parts, can be written
is the electron-ion drift velocity. We saw in Section 7.5 that,
in the absence of drift, the ion acoustic wave is damped. We now wish to investigate whether the presence of an electron-ion drift (which is associated with
a net current flowing in the plasma) can destabilize the mode. The appropriate dispersion relation is Equation (7.49), which, on
integration by parts, can be written
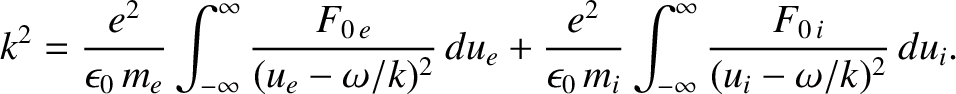 |
(7.136) |
The previous three equations can be combined together, and the integrals performed as contour integrals in the complex 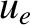 and
and 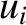 planes (closed in the lower halves of these planes), making use of the residue theorem (Riley 1974), to give
planes (closed in the lower halves of these planes), making use of the residue theorem (Riley 1974), to give
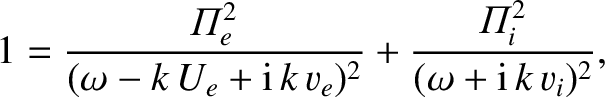 |
(7.137) |
where we have assumed that 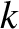 is real and positive, and that
is real and positive, and that 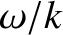 lies in the upper half of the complex plane.
In the limit
lies in the upper half of the complex plane.
In the limit
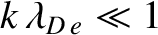 , where
, where
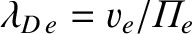 , the left-hand side of the previous expression is
negligible compared to the two terms on the right-hand side, and we obtain
, the left-hand side of the previous expression is
negligible compared to the two terms on the right-hand side, and we obtain
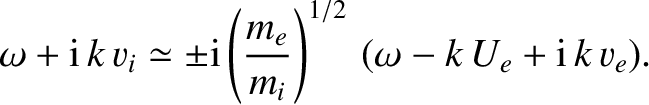 |
(7.138) |
Choosing the negative sign, which ensures that the phase-velocity is in the correct direction, we get
![$\displaystyle \omega\simeq k\left(\frac{m_e}{m_i}\right)^{1/2}v_e + {\rm i}\,k\left[\left(\frac{m_e}{m_i}\right)^{1/2}U_e-v_i\right].$](img2567.png) |
(7.139) |
If we write
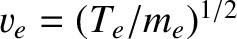 and
and
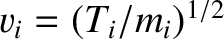 , where
, where 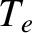 and
and 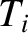 are the effective electron and ion temperatures,
then the previous expression yields
are the effective electron and ion temperatures,
then the previous expression yields
![$\displaystyle \omega\simeq k\left(\frac{T_e}{m_i}\right)^{1/2} + {\rm i}\,k\lef...
...ac{m_e}{m_i}\right)^{1/2}\left[U_e - \left(\frac{T_i}{m_e}\right)^{1/2}\right].$](img2570.png) |
(7.140) |
Thus, the phase-velocity of the wave is
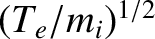 , whereas the growth-rate is
, whereas the growth-rate is
![$\displaystyle \gamma = k\left(\frac{m_e}{m_i}\right)^{1/2}\left[U_e - \left(\frac{T_i}{m_e}\right)^{1/2}\right].$](img2571.png) |
(7.141) |
It can be seen that the growth-rate becomes positive (i.e., the mode becomes unstable) when the drift velocity exceeds the
critical value
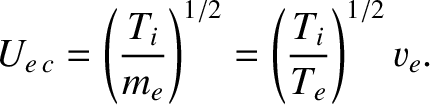 |
(7.142) |
This calculation indicates that if the electron and ion temperatures are similar then the threshold
drift velocity is of order the electron thermal speed, which is usually very large. In other words,
a significant current is generally required to drive the ion acoustic wave unstable. The instability threshold (relative to the electron thermal speed)
is considerably reduced if the electron temperature greatly exceeds the ion temperature.
If we repeat the previous calculation using the more realistic Maxwellian velocity distributions,
![$\displaystyle F_{0\,e}(u_e) = \frac{n}{(2\pi\,T_e/m_e)^{1/2}}\exp\left[-\frac{m_e\,(u_e-U_e)^{2}}{2\,T_e}\right],$](img2573.png) |
(7.143) |
and
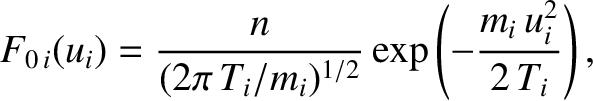 |
(7.144) |
then the dispersion relation (7.136) yields
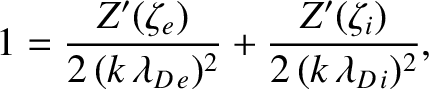 |
(7.145) |
where
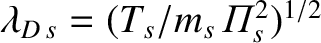 ,
,
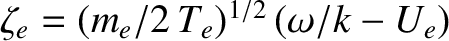 , and
, and
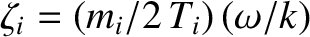 . As in Section 7.5, we assume that the phase-velocity of the wave is much
less than the electron thermal velocity, but much greater than the ion thermal velocity. This implies that
. As in Section 7.5, we assume that the phase-velocity of the wave is much
less than the electron thermal velocity, but much greater than the ion thermal velocity. This implies that
 and
and
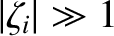 .
Using the
small-argument expansion
.
Using the
small-argument expansion
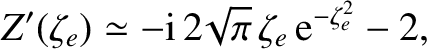 |
(7.146) |
and the large-argument expansion
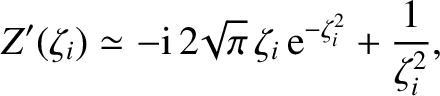 |
(7.147) |
we obtain
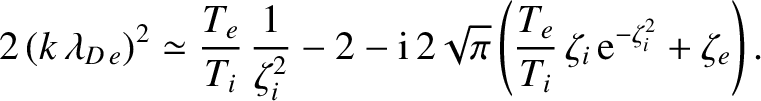 |
(7.148) |
In the limit
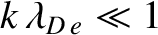 , the previous expression yields
, the previous expression yields
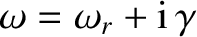 ,
where
,
where
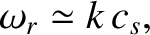 |
(7.149) |
and
![$\displaystyle \frac{\gamma}{\omega_r} \simeq -\sqrt{\frac{\pi}{8}}\left[\left(\...
...\left(\frac{T_e}{T_i}\right)^{3/2}
\exp\left(-\frac{T_e}{2\,T_i}\right)\right],$](img2586.png) |
(7.150) |
Here,
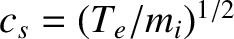 is the phase-velocity of the ion acoustic wave, and it is assumed that
is the phase-velocity of the ion acoustic wave, and it is assumed that
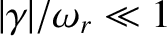 . The ion acoustic wave phase-velocity is
much less than the electron thermal speed, as previously assumed, but is only much greater than the ion thermal
speed if
. The ion acoustic wave phase-velocity is
much less than the electron thermal speed, as previously assumed, but is only much greater than the ion thermal
speed if
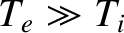 . According to Equation (7.150), the threshold
electron-ion drift speed above which the ion acoustic wave is destabilized is
. According to Equation (7.150), the threshold
electron-ion drift speed above which the ion acoustic wave is destabilized is
![$\displaystyle U_{e\,c}= c_s\left[1+\left(\frac{m_i}{m_e}\right)^{1/2}\,\left(\frac{T_e}{T_i}\right)^{3/2}
\exp\left(-\frac{T_e}{2\,T_i}\right)\right].$](img2589.png) |
(7.151) |
As before, this formula (which is only accurate when
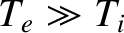 ) indicates that the threshold is strongly reduced (relative to
) indicates that the threshold is strongly reduced (relative to 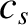 ) as the ratio of the electron to the ion temperature is increased.
) as the ratio of the electron to the ion temperature is increased.
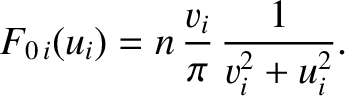
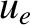 and
and 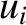 are the parallel (to
are the parallel (to 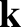 ) electron and ion velocities, respectively,
) electron and ion velocities, respectively, 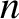 is the particle number density,
is the particle number density,
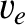 and
and 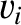 are the electron and ion thermal spreads, respectively, and
are the electron and ion thermal spreads, respectively, and 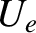 is the electron-ion drift velocity. We saw in Section 7.5 that,
in the absence of drift, the ion acoustic wave is damped. We now wish to investigate whether the presence of an electron-ion drift (which is associated with
a net current flowing in the plasma) can destabilize the mode. The appropriate dispersion relation is Equation (7.49), which, on
integration by parts, can be written
The previous three equations can be combined together, and the integrals performed as contour integrals in the complex
is the electron-ion drift velocity. We saw in Section 7.5 that,
in the absence of drift, the ion acoustic wave is damped. We now wish to investigate whether the presence of an electron-ion drift (which is associated with
a net current flowing in the plasma) can destabilize the mode. The appropriate dispersion relation is Equation (7.49), which, on
integration by parts, can be written
The previous three equations can be combined together, and the integrals performed as contour integrals in the complex 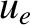 and
and 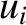 planes (closed in the lower halves of these planes), making use of the residue theorem (Riley 1974), to give
where we have assumed that
planes (closed in the lower halves of these planes), making use of the residue theorem (Riley 1974), to give
where we have assumed that 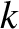 is real and positive, and that
is real and positive, and that 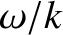 lies in the upper half of the complex plane.
In the limit
lies in the upper half of the complex plane.
In the limit
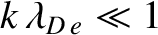 , where
, where
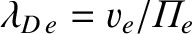 , the left-hand side of the previous expression is
negligible compared to the two terms on the right-hand side, and we obtain
, the left-hand side of the previous expression is
negligible compared to the two terms on the right-hand side, and we obtain
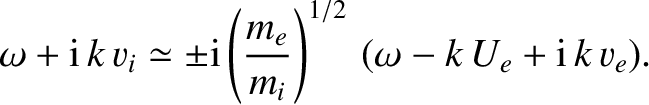
![$\displaystyle \omega\simeq k\left(\frac{m_e}{m_i}\right)^{1/2}v_e + {\rm i}\,k\left[\left(\frac{m_e}{m_i}\right)^{1/2}U_e-v_i\right].$](img2567.png)
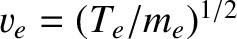 and
and
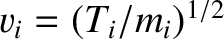 , where
, where 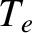 and
and 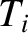 are the effective electron and ion temperatures,
then the previous expression yields
are the effective electron and ion temperatures,
then the previous expression yields
![$\displaystyle \omega\simeq k\left(\frac{T_e}{m_i}\right)^{1/2} + {\rm i}\,k\lef...
...ac{m_e}{m_i}\right)^{1/2}\left[U_e - \left(\frac{T_i}{m_e}\right)^{1/2}\right].$](img2570.png)
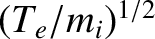 , whereas the growth-rate is
, whereas the growth-rate is
![$\displaystyle \gamma = k\left(\frac{m_e}{m_i}\right)^{1/2}\left[U_e - \left(\frac{T_i}{m_e}\right)^{1/2}\right].$](img2571.png)
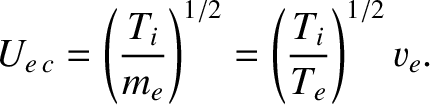
![$\displaystyle F_{0\,e}(u_e) = \frac{n}{(2\pi\,T_e/m_e)^{1/2}}\exp\left[-\frac{m_e\,(u_e-U_e)^{2}}{2\,T_e}\right],$](img2573.png)
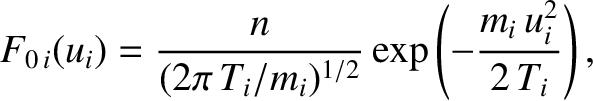
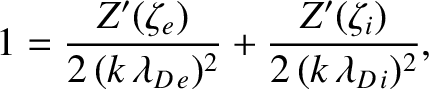
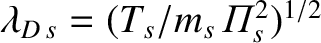 ,
,
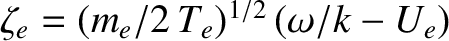 , and
, and
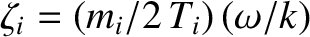 . As in Section 7.5, we assume that the phase-velocity of the wave is much
less than the electron thermal velocity, but much greater than the ion thermal velocity. This implies that
. As in Section 7.5, we assume that the phase-velocity of the wave is much
less than the electron thermal velocity, but much greater than the ion thermal velocity. This implies that
 and
and
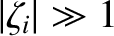 .
Using the
small-argument expansion
.
Using the
small-argument expansion
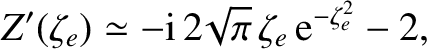
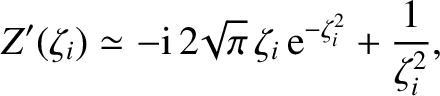
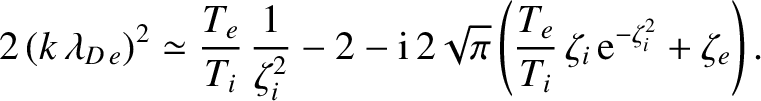
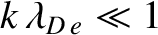 , the previous expression yields
, the previous expression yields
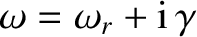 ,
where
,
where
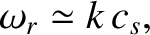
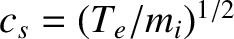 is the phase-velocity of the ion acoustic wave, and it is assumed that
is the phase-velocity of the ion acoustic wave, and it is assumed that
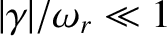 . The ion acoustic wave phase-velocity is
much less than the electron thermal speed, as previously assumed, but is only much greater than the ion thermal
speed if
. The ion acoustic wave phase-velocity is
much less than the electron thermal speed, as previously assumed, but is only much greater than the ion thermal
speed if
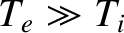 . According to Equation (7.150), the threshold
electron-ion drift speed above which the ion acoustic wave is destabilized is
. According to Equation (7.150), the threshold
electron-ion drift speed above which the ion acoustic wave is destabilized is
![$\displaystyle U_{e\,c}= c_s\left[1+\left(\frac{m_i}{m_e}\right)^{1/2}\,\left(\frac{T_e}{T_i}\right)^{3/2}
\exp\left(-\frac{T_e}{2\,T_i}\right)\right].$](img2589.png)
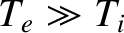 ) indicates that the threshold is strongly reduced (relative to
) indicates that the threshold is strongly reduced (relative to 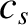 ) as the ratio of the electron to the ion temperature is increased.
) as the ratio of the electron to the ion temperature is increased.