Next: Perpendicular Wave Propagation Up: Waves in Warm Plasmas Previous: Waves in Magnetized Plasmas Contents
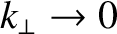 , and, hence, from Equation (7.84),
, and, hence, from Equation (7.84),
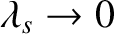 .
Making use of Equation (7.88), the matrix
.
Making use of Equation (7.88), the matrix
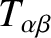 simplifies to
simplifies to
![$\displaystyle T_{\alpha\beta} = \left( \begin{array}{ccc}
[Z(\xi_1)+Z(\xi_{-1})...
...)+Z(\xi_{-1})]/2, & 0 \\ [0.5ex]
0, & 0,
&-Z'(\xi_0)\,\xi_0
\end{array}\right),$](img2441.png) |
(7.92) |
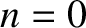 and
and 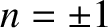 .
The dispersion relation can be written [see Equations (5.9) and (5.10)]
where
and
.
The dispersion relation can be written [see Equations (5.9) and (5.10)]
where
and
 .
.
The first root of Equation (7.93) is
with the eigenvector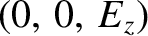 .
Here, use has been made of Equation (7.41).
This root evidentially corresponds to
a longitudinal, electrostatic plasma wave. In fact, it is easily
demonstrated that Equation (7.97) is equivalent to the dispersion relation
(7.49) that we found earlier for electrostatic
plasma waves, for the special case in which the distribution
functions are Maxwellians. The analysis of Section 7.4 implies that the
electrostatic wave described by the previous expression is subject to
significant damping whenever the argument of the plasma dispersion
function becomes less than or comparable with unity: that is, whenever
.
Here, use has been made of Equation (7.41).
This root evidentially corresponds to
a longitudinal, electrostatic plasma wave. In fact, it is easily
demonstrated that Equation (7.97) is equivalent to the dispersion relation
(7.49) that we found earlier for electrostatic
plasma waves, for the special case in which the distribution
functions are Maxwellians. The analysis of Section 7.4 implies that the
electrostatic wave described by the previous expression is subject to
significant damping whenever the argument of the plasma dispersion
function becomes less than or comparable with unity: that is, whenever
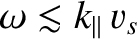 .
.
The second and third roots of Equation (7.93) are
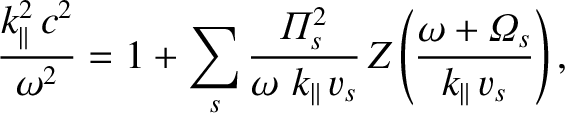 |
(7.98) |
 , and
, and
 |
(7.99) |
 . The former root evidently
corresponds to a right-handed circularly polarized wave, whereas the latter
root corresponds to a left-handed circularly polarized wave.
The previous two dispersion relations are essentially the same as the corresponding
fluid dispersion relations, (5.90) and (5.91), except that they explicitly
contain collisionless damping at the cyclotron resonances. Roughly speaking, the
damping is significant whenever the arguments of the plasma dispersion functions
are less than or of order unity. This corresponds to
. The former root evidently
corresponds to a right-handed circularly polarized wave, whereas the latter
root corresponds to a left-handed circularly polarized wave.
The previous two dispersion relations are essentially the same as the corresponding
fluid dispersion relations, (5.90) and (5.91), except that they explicitly
contain collisionless damping at the cyclotron resonances. Roughly speaking, the
damping is significant whenever the arguments of the plasma dispersion functions
are less than or of order unity. This corresponds to
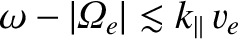 |
(7.100) |
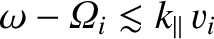 |
(7.101) |
The collisionless cyclotron damping mechanism is similar to the Landau damping mechanism for longitudinal waves discussed in Section 7.3. In the former case, the resonant particles are those that gyrate about the magnetic field at approximately the same angular frequency as the wave electric field. Note that, in kinetic theory, the cyclotron resonances possess a finite width in frequency space (i.e., the incident wave does not have to oscillate at exactly the cyclotron frequency in order for there to be an absorption of wave energy by the plasma), unlike in the cold plasma model, where the resonances possess zero width.