Next: Magnetized Plasmas Up: Plasma Parameters Previous: Plasma Parameter Contents
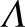 we can speak of binary collisions, and therefore of
a collision frequency, denoted by
we can speak of binary collisions, and therefore of
a collision frequency, denoted by 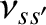 . Here,
. Here,
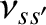 measures the rate at which particles of species
measures the rate at which particles of species  are scattered
by those of species
are scattered
by those of species 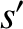 . When specifying only a single subscript, one is
generally referring to the total collision rate for that species,
including impacts with all other species. Very roughly,
. When specifying only a single subscript, one is
generally referring to the total collision rate for that species,
including impacts with all other species. Very roughly,
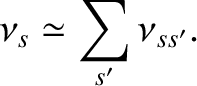 |
(1.21) |
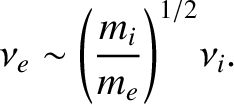 |
(1.22) |
 , measures the frequency with which a
particle trajectory undergoes a major angular change due to
Coulomb interactions with other particles. Coulomb collisions are, in fact,
predominately small angle scattering events, so the collision frequency
is not the inverse of the typical time between collisions. (See Chapter 3.) Instead, it is
the inverse of the typical time needed for enough collisions to occur that the particle trajectory is deviated through
, measures the frequency with which a
particle trajectory undergoes a major angular change due to
Coulomb interactions with other particles. Coulomb collisions are, in fact,
predominately small angle scattering events, so the collision frequency
is not the inverse of the typical time between collisions. (See Chapter 3.) Instead, it is
the inverse of the typical time needed for enough collisions to occur that the particle trajectory is deviated through 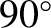 .
For this reason, the collision frequency is sometimes termed the
.
For this reason, the collision frequency is sometimes termed the 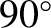 scattering
rate.
scattering
rate.
It is conventional to define the mean-free-path,
Clearly, the mean-free-path measures the typical distance a particle travels between “collisions” (i.e.,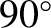 scattering events). A collision-dominated, or collisional,
plasma is simply one in which
scattering events). A collision-dominated, or collisional,
plasma is simply one in which
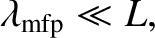 |
(1.24) |
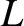 is the observation lengthscale. The opposite limit of
long mean-free-path is said to correspond to a collisionless plasma.
Collisions greatly simplify plasma behavior by driving the system toward
statistical equilibrium, characterized by Maxwellian distribution
functions. (See Section 3.11.) Furthermore, short mean-free-paths generally ensure that plasma
transport is local (i.e., diffusive) in nature, which is a considerable
simplification.
is the observation lengthscale. The opposite limit of
long mean-free-path is said to correspond to a collisionless plasma.
Collisions greatly simplify plasma behavior by driving the system toward
statistical equilibrium, characterized by Maxwellian distribution
functions. (See Section 3.11.) Furthermore, short mean-free-paths generally ensure that plasma
transport is local (i.e., diffusive) in nature, which is a considerable
simplification.
The typical magnitude of the collision frequency is (see Section 3.14)
Note that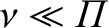 in a weakly coupled plasma. It follows that
collisions do not seriously interfere with plasma oscillations in such systems.
On the other hand, Equation (1.25) implies that
in a weakly coupled plasma. It follows that
collisions do not seriously interfere with plasma oscillations in such systems.
On the other hand, Equation (1.25) implies that
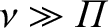 in a strongly
coupled plasma, suggesting that collisions effectively prevent plasma
oscillations in such systems. This accords well with our basic picture of a strongly
coupled plasma as a system,
dominated by Coulomb interactions, that does not exhibit conventional
plasma dynamics.
in a strongly
coupled plasma, suggesting that collisions effectively prevent plasma
oscillations in such systems. This accords well with our basic picture of a strongly
coupled plasma as a system,
dominated by Coulomb interactions, that does not exhibit conventional
plasma dynamics.
Equations (1.7), (1.23), and (1.25) imply that the ratio of the mean-free-path to the Debye length can be written
 |
(1.26) |
Equations (1.5) and (1.20) yield
Thus, diffuse, high temperature plasmas tend to be collisionless, whereas dense, low temperature plasmas are more likely to be collisional.While collisions are crucial to the confinement and dynamics of neutral gases, they play a far less important role in plasmas. In fact, in many plasmas the magnetic field effectively plays the role that collisions play in a neutral gas. In such plasmas, charged particles are constrained from moving perpendicular to the field by their small Larmor orbits, rather than by collisions. Confinement along the field-lines is more difficult to achieve, unless the field-lines form closed loops (or closed surfaces). Thus, it makes sense to talk about a “collisionless plasma,” whereas it makes little sense to talk about a “collisionless neutral gas.” Many plasmas are collisionless to a very good approximation, especially those encountered in astrophysics and space plasma physics contexts.