Next: Plasma Beta Up: Plasma Parameters Previous: Collisions Contents
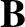 , is strong enough to significantly alter particle
trajectories. In particular,
magnetized plasmas are highly anisotropic, responding differently to
forces that are parallel and perpendicular to the direction
of
, is strong enough to significantly alter particle
trajectories. In particular,
magnetized plasmas are highly anisotropic, responding differently to
forces that are parallel and perpendicular to the direction
of 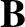 . Incidentally, a magnetized plasma moving with
mean velocity
. Incidentally, a magnetized plasma moving with
mean velocity 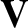 contains an electric field
contains an electric field
 that is not affected
by Debye shielding. Of course, the electric
field is essentially zero in the rest frame of the plasma.
that is not affected
by Debye shielding. Of course, the electric
field is essentially zero in the rest frame of the plasma.
As is well known, charged particles respond to the Lorentz force,
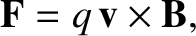 |
(1.28) |
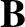 , while executing
circular Larmor orbits, or gyro-orbits, in the plane perpendicular to
, while executing
circular Larmor orbits, or gyro-orbits, in the plane perpendicular to 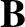 (Fitzpatrick 2008).
As the field-strength increases, the resulting helical orbits become more
tightly wound, effectively tying particles to magnetic field-lines.
(Fitzpatrick 2008).
As the field-strength increases, the resulting helical orbits become more
tightly wound, effectively tying particles to magnetic field-lines.
The typical Larmor radius, or gyroradius, of a charged particle gyrating in a magnetic field is given by
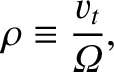 |
(1.29) |
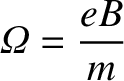 |
(1.30) |
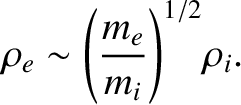 |
(1.31) |
A plasma system, or process, is said to be magnetized if its
characteristic lengthscale, 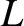 , is large compared to the gyroradius.
In the opposite limit,
, is large compared to the gyroradius.
In the opposite limit, 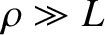 , charged particles have essentially
straight-line trajectories. Thus, the ability of the magnetic field to
significantly affect particle trajectories is measured by the
magnetization parameter,
, charged particles have essentially
straight-line trajectories. Thus, the ability of the magnetic field to
significantly affect particle trajectories is measured by the
magnetization parameter,
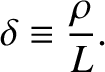 |
(1.32) |
There are some cases of interest in which the electrons are magnetized, but the ions are not. However, a “magnetized” plasma conventionally refers to one in which both species are magnetized. This state is generally achieved when
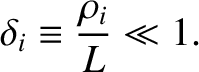 |
(1.33) |