Collisional Conservation Laws
Consider
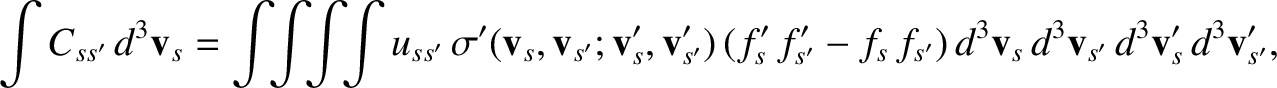 |
(3.28) |
which follows from Equation (3.23).
Interchanging primed and unprimed dummy variables of integration on the right-hand side, we
obtain
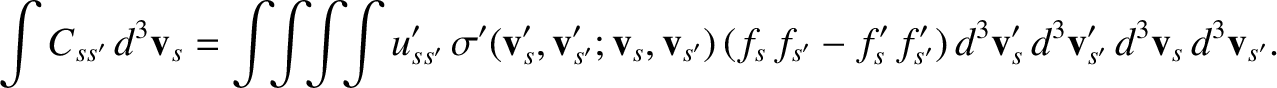 |
(3.29) |
Hence, making use of Equation (3.18), as well as the fact that
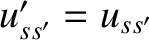 , we
deduce that
which implies that
, we
deduce that
which implies that
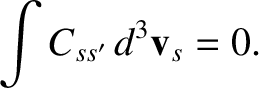 |
(3.31) |
The previous expression states that collisions with species- particles give rise to zero net rate of change of the number density of species-
particles give rise to zero net rate of change of the number density of species- particles
at position
particles
at position 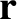 and time
and time 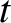 . In other words, the collisions conserve the number of species-
. In other words, the collisions conserve the number of species- particles.
Now, it is easily seen from Equations (3.23) and (3.24) that
particles.
Now, it is easily seen from Equations (3.23) and (3.24) that
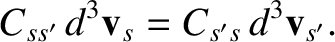 |
(3.32) |
Hence, Equation (3.31) also implies that
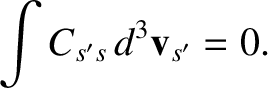 |
(3.33) |
In other words, collisions also conserve the number of species- particles.
particles.
Consider
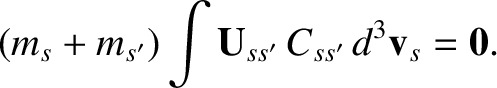 |
(3.34) |
This integral is obviously zero, as indicated, as a consequence of the conservation law (3.31), as well as the fact that the center
of mass velocity,
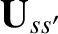 , is a constant of the motion. However, making use of Equations (3.10) and (3.32), the
previous expression can be rewritten in the form
, is a constant of the motion. However, making use of Equations (3.10) and (3.32), the
previous expression can be rewritten in the form
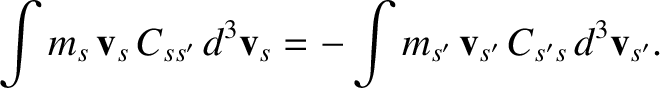 |
(3.35) |
This equation states that the rate at which species- particles gain momentum due to collisions with species-
particles gain momentum due to collisions with species- particles is equal
to the rate at which species-
particles is equal
to the rate at which species- particles lose momentum due to collisions with species-
particles lose momentum due to collisions with species- particles. In other words, the collisions
conserve momentum.
particles. In other words, the collisions
conserve momentum.
Finally, consider
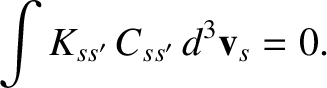 |
(3.36) |
This integral is obviously zero, as indicated, as a consequence of the conservation law (3.31), as well as the fact that the kinetic
energy, 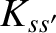 , is the same before and after an elastic collision. It follows from Equations (3.15) and (3.32) that
, is the same before and after an elastic collision. It follows from Equations (3.15) and (3.32) that
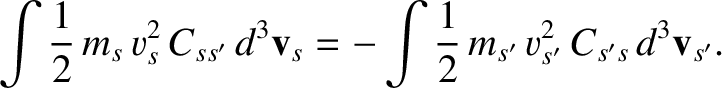 |
(3.37) |
This equation states that the rate at which species- particles gain kinetic energy due to collisions with species-
particles gain kinetic energy due to collisions with species- particles is equal
to the rate at which species-
particles is equal
to the rate at which species- particles lose kinetic energy due to collisions with species-
particles lose kinetic energy due to collisions with species- particles.
In other words, the collisions conserve energy.
particles.
In other words, the collisions conserve energy.
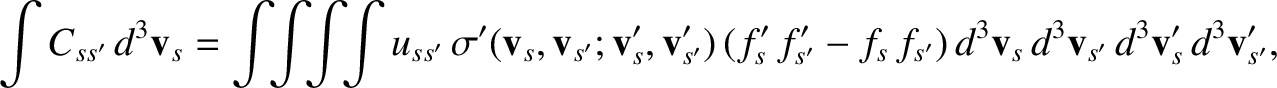
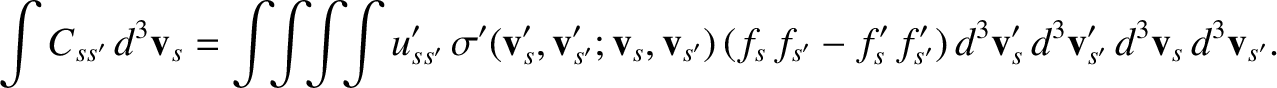
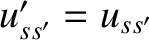 , we
deduce that
, we
deduce that
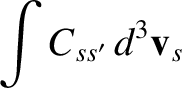
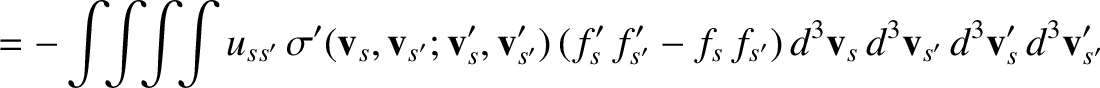
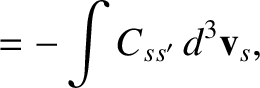
 particles give rise to zero net rate of change of the number density of species-
particles give rise to zero net rate of change of the number density of species- particles
at position
particles
at position 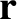 and time
and time 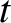 . In other words, the collisions conserve the number of species-
. In other words, the collisions conserve the number of species- particles.
Now, it is easily seen from Equations (3.23) and (3.24) that
Hence, Equation (3.31) also implies that
particles.
Now, it is easily seen from Equations (3.23) and (3.24) that
Hence, Equation (3.31) also implies that
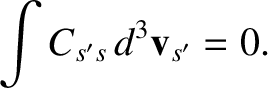
 particles.
particles.
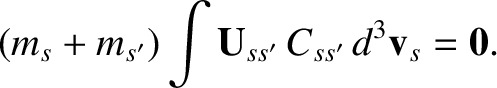
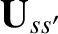 , is a constant of the motion. However, making use of Equations (3.10) and (3.32), the
previous expression can be rewritten in the form
This equation states that the rate at which species-
, is a constant of the motion. However, making use of Equations (3.10) and (3.32), the
previous expression can be rewritten in the form
This equation states that the rate at which species- particles gain momentum due to collisions with species-
particles gain momentum due to collisions with species- particles is equal
to the rate at which species-
particles is equal
to the rate at which species- particles lose momentum due to collisions with species-
particles lose momentum due to collisions with species- particles. In other words, the collisions
conserve momentum.
particles. In other words, the collisions
conserve momentum.
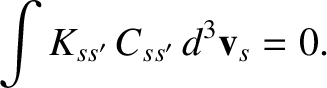
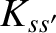 , is the same before and after an elastic collision. It follows from Equations (3.15) and (3.32) that
This equation states that the rate at which species-
, is the same before and after an elastic collision. It follows from Equations (3.15) and (3.32) that
This equation states that the rate at which species- particles gain kinetic energy due to collisions with species-
particles gain kinetic energy due to collisions with species- particles is equal
to the rate at which species-
particles is equal
to the rate at which species- particles lose kinetic energy due to collisions with species-
particles lose kinetic energy due to collisions with species- particles.
In other words, the collisions conserve energy.
particles.
In other words, the collisions conserve energy.