Next: Boltzmann Collision Operator Up: Collisions Previous: Collision Operator Contents
 particle and a species-
particle and a species-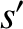 particle. Let the mass and instantaneous velocity of the former particle be
particle. Let the mass and instantaneous velocity of the former particle be 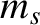 and
and  , respectively. Likewise, let the
mass and
instantaneous velocity of the latter particle be
, respectively. Likewise, let the
mass and
instantaneous velocity of the latter particle be 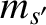 and
and
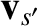 , respectively. The velocity of the
center of mass is given by
Moreover, conservation of momentum implies that
, respectively. The velocity of the
center of mass is given by
Moreover, conservation of momentum implies that
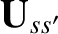 is a constant of the motion. The relative velocity is
defined
is a constant of the motion. The relative velocity is
defined
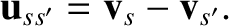 |
(3.11) |
 and
and
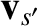 in terms of
in terms of
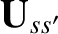 and
and
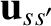 as follows:
Here,
as follows:
Here,
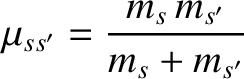 |
(3.14) |
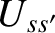 is constant, we deduce that the
magnitude of the relative velocity,
is constant, we deduce that the
magnitude of the relative velocity, 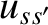 , is also the same before and after such a collision. Thus, it is only the direction of the
relative velocity vector, rather than its length, that changes during an elastic collision.
, is also the same before and after such a collision. Thus, it is only the direction of the
relative velocity vector, rather than its length, that changes during an elastic collision.