Next: Waves in Inhomogeneous Plasmas Up: Waves in Cold Plasmas Previous: Perpendicular Wave Propagation Contents
![$\exp[\,{\rm i}\,({\bf k}\cdot{\bf r}-\omega\,t)]$](img1871.png) the equations
the equations
 and
and
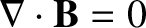 follow from Equations (5.4) and (5.5). This
explains why the former equations are not explicitly used in the study of plane waves.
follow from Equations (5.4) and (5.5). This
explains why the former equations are not explicitly used in the study of plane waves.

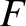 , defined in Equation (5.48), can be
written in the positive definite form
, defined in Equation (5.48), can be
written in the positive definite form
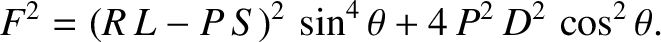
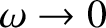 ,
,
 |
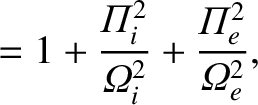 |
|
 |
 |
|
 |
 |
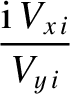 |
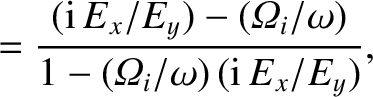 |
|
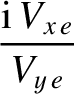 |
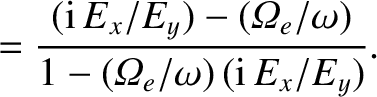 |
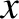 -
-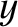 plane in the electron/ion
cyclotron direction.
plane in the electron/ion
cyclotron direction.
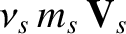 to the equation of motion of species
to the equation of motion of species  . Here,
. Here, 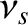 is the effective collision
frequency for species
is the effective collision
frequency for species  , where
, where  stands for either
stands for either 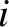 or
or 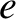 . Thus, the species
. Thus, the species  equation of motion
becomes
equation of motion
becomes
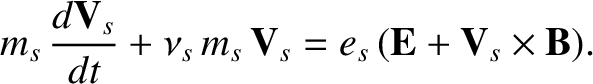
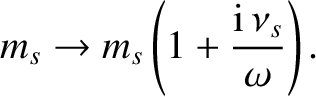
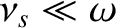 , and
, and
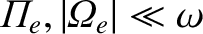 , show that
the real and imaginary parts of the wavenumber are
, show that
the real and imaginary parts of the wavenumber are
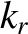 |
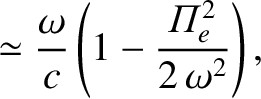 |
|
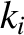 |
 |

 . These oscillations have the
same frequency irrespective of the wavevector,
. These oscillations have the
same frequency irrespective of the wavevector, 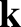 . However, when
pressure is included in the analysis, the frequency of the oscillation
starts to depend on
. However, when
pressure is included in the analysis, the frequency of the oscillation
starts to depend on 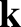 . We can investigate this effect by treating the
(singly-charged) ions as stationary neutralizing fluid of number density
. We can investigate this effect by treating the
(singly-charged) ions as stationary neutralizing fluid of number density 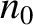 .
The electron fluid equations are written
.
The electron fluid equations are written
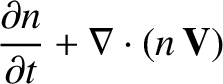 |
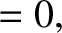 |
|
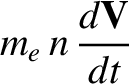 |
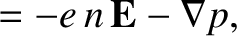 |
|
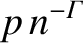 |
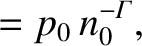 |
|
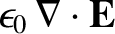 |
 |
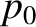 and
and
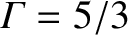 are constants. Let
are constants. Let 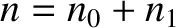 ,
,
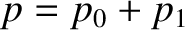 ,
,
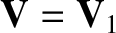 , and
, and
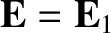 , where
the subscript 0 denotes an equilibrium quantity, and the subscript
, where
the subscript 0 denotes an equilibrium quantity, and the subscript 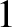 denotes
a small perturbation. Develop a set of linear equations sufficient to solve
for the perturbed variables. Assuming that all perturbed quantities vary in space and time as
denotes
a small perturbation. Develop a set of linear equations sufficient to solve
for the perturbed variables. Assuming that all perturbed quantities vary in space and time as
![$\exp[\,{\rm i}\,({\bf k}\cdot{\bf r}-\omega\,t)]$](img1871.png) , find the dispersion relation linking
, find the dispersion relation linking 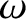 and
and 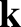 . Find expressions for the phase-velocity and group-velocity of
the wave as functions of
. Find expressions for the phase-velocity and group-velocity of
the wave as functions of 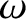 .
.