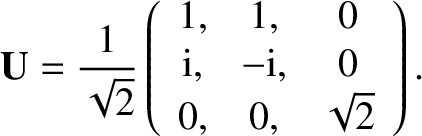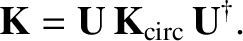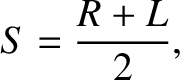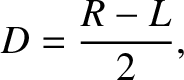Cold-Plasma Dielectric Permittivity
In a collisionless plasma, the linearized cold-plasma equations
are written [see Equations (4.225)–(4.227)],
where 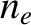 is the equilibrium electron number density.
Substitution of plane-wave solutions of the type (5.1) into the previous
equations yields
Let
be the electron plasma frequency, the ion plasma frequency,
the electron cyclotron frequency, and the ion cyclotron frequency,
respectively. Eliminating the
fluid velocity,
is the equilibrium electron number density.
Substitution of plane-wave solutions of the type (5.1) into the previous
equations yields
Let
be the electron plasma frequency, the ion plasma frequency,
the electron cyclotron frequency, and the ion cyclotron frequency,
respectively. Eliminating the
fluid velocity, 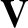 , between Equations (5.14) and (5.15), and making
use of the previous definitions, we obtain
, between Equations (5.14) and (5.15), and making
use of the previous definitions, we obtain
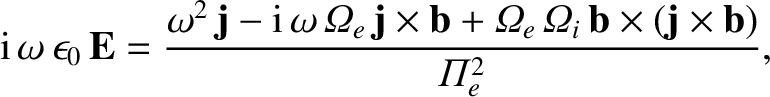 |
(5.20) |
where
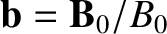 .
.
The parallel component of the previous equation is readily solved to give
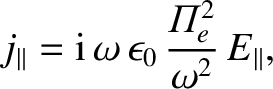 |
(5.21) |
where
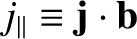 , et cetera.
In solving for
, et cetera.
In solving for
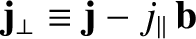 , it is helpful to define the
vectors
Here,
, it is helpful to define the
vectors
Here,
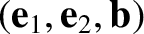 are a
set of mutually orthogonal, right-handed
unit vectors. It is easily demonstrated that
It follows that
are a
set of mutually orthogonal, right-handed
unit vectors. It is easily demonstrated that
It follows that
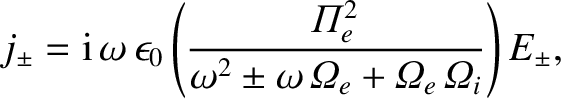 |
(5.26) |
where
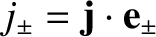 , et cetera.
, et cetera.
The conductivity tensor is diagonal in the “circular” basis
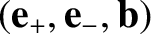 . In fact, its elements are the coefficients of
. In fact, its elements are the coefficients of 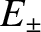 and
and
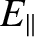 in Equations (5.26) and (5.21), respectively. Thus,
the dielectric permittivity tensor, defined in Equation (5.8), takes the form
in Equations (5.26) and (5.21), respectively. Thus,
the dielectric permittivity tensor, defined in Equation (5.8), takes the form
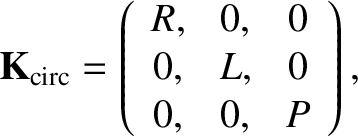 |
(5.27) |
where
Here, 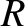 and
and 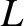 represent the permittivities for right- and left-handed
circularly polarized waves, respectively. The permittivity parallel to the
magnetic field,
represent the permittivities for right- and left-handed
circularly polarized waves, respectively. The permittivity parallel to the
magnetic field, 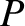 , is identical to that of an unmagnetized plasma.
, is identical to that of an unmagnetized plasma.
The previous expressions are only approximate because the small
mass-ratio ordering
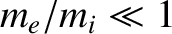 has already been incorporated into the
cold-plasma equations. The exact expressions, which are most easily
obtained by solving the individual charged particle equations
of motion, and then summing to obtain the
fluid response, are
has already been incorporated into the
cold-plasma equations. The exact expressions, which are most easily
obtained by solving the individual charged particle equations
of motion, and then summing to obtain the
fluid response, are
Equations (5.28)–(5.30) and (5.31)–(5.33) are equivalent in the limit
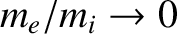 .
Furthermore, Equations (5.31)–(5.33) generalize in a fairly obvious manner to plasmas
consisting of more than two particle species.
.
Furthermore, Equations (5.31)–(5.33) generalize in a fairly obvious manner to plasmas
consisting of more than two particle species.
In order to obtain the standard expression for dielectric permittivity tensor, it is necessary
to transform to the Cartesian basis
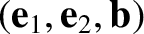 .
Let
.
Let
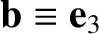 , for ease of notation. It follows that
the components of an arbitrary vector
, for ease of notation. It follows that
the components of an arbitrary vector 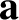 in the Cartesian basis are
related to the components in the “circular” basis via
in the Cartesian basis are
related to the components in the “circular” basis via
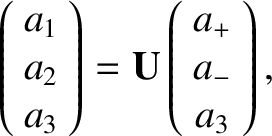 |
(5.34) |
where the unitary transformation matrix 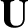 is written
is written
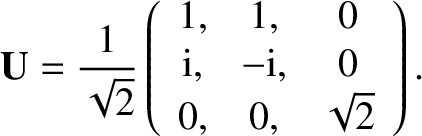 |
(5.35) |
The dielectric permittivity in the Cartesian basis is then
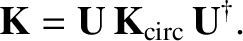 |
(5.36) |
We obtain
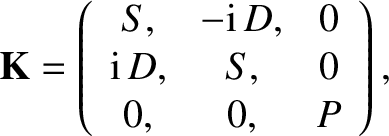 |
(5.37) |
where
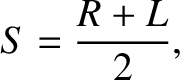 |
(5.38) |
and
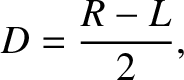 |
(5.39) |
represent the sum and difference of the right- and left-handed dielectric
permittivities, respectively.
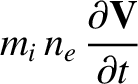
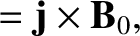
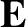
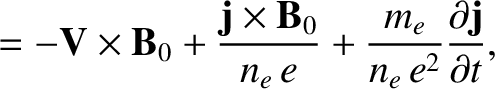
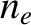 is the equilibrium electron number density.
Substitution of plane-wave solutions of the type (5.1) into the previous
equations yields
Let
be the electron plasma frequency, the ion plasma frequency,
the electron cyclotron frequency, and the ion cyclotron frequency,
respectively. Eliminating the
fluid velocity,
is the equilibrium electron number density.
Substitution of plane-wave solutions of the type (5.1) into the previous
equations yields
Let
be the electron plasma frequency, the ion plasma frequency,
the electron cyclotron frequency, and the ion cyclotron frequency,
respectively. Eliminating the
fluid velocity, 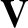 , between Equations (5.14) and (5.15), and making
use of the previous definitions, we obtain
, between Equations (5.14) and (5.15), and making
use of the previous definitions, we obtain
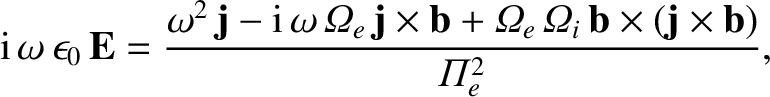
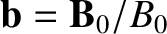 .
.
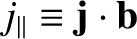 , et cetera.
In solving for
, et cetera.
In solving for
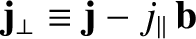 , it is helpful to define the
vectors
, it is helpful to define the
vectors
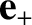
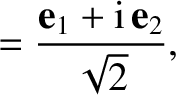
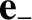
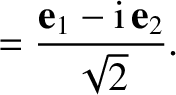
 are a
set of mutually orthogonal, right-handed
unit vectors. It is easily demonstrated that
are a
set of mutually orthogonal, right-handed
unit vectors. It is easily demonstrated that
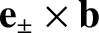
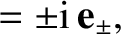
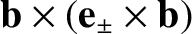
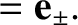
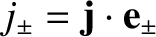 , et cetera.
, et cetera.
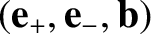 . In fact, its elements are the coefficients of
. In fact, its elements are the coefficients of 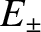 and
and
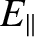 in Equations (5.26) and (5.21), respectively. Thus,
the dielectric permittivity tensor, defined in Equation (5.8), takes the form
in Equations (5.26) and (5.21), respectively. Thus,
the dielectric permittivity tensor, defined in Equation (5.8), takes the form
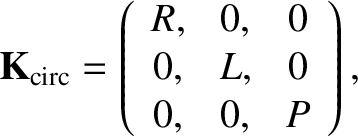
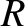 and
and 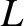 represent the permittivities for right- and left-handed
circularly polarized waves, respectively. The permittivity parallel to the
magnetic field,
represent the permittivities for right- and left-handed
circularly polarized waves, respectively. The permittivity parallel to the
magnetic field, 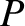 , is identical to that of an unmagnetized plasma.
, is identical to that of an unmagnetized plasma.
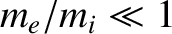 has already been incorporated into the
cold-plasma equations. The exact expressions, which are most easily
obtained by solving the individual charged particle equations
of motion, and then summing to obtain the
fluid response, are
has already been incorporated into the
cold-plasma equations. The exact expressions, which are most easily
obtained by solving the individual charged particle equations
of motion, and then summing to obtain the
fluid response, are
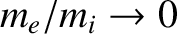 .
Furthermore, Equations (5.31)–(5.33) generalize in a fairly obvious manner to plasmas
consisting of more than two particle species.
.
Furthermore, Equations (5.31)–(5.33) generalize in a fairly obvious manner to plasmas
consisting of more than two particle species.
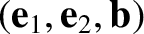 .
Let
.
Let
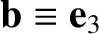 , for ease of notation. It follows that
the components of an arbitrary vector
, for ease of notation. It follows that
the components of an arbitrary vector 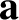 in the Cartesian basis are
related to the components in the “circular” basis via
in the Cartesian basis are
related to the components in the “circular” basis via
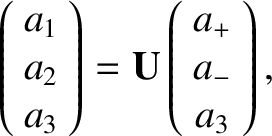
 is written
is written