Next: Boltzmann H-Theorem Up: Collisions Previous: Rosenbluth Potentials Contents
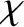 is small,
Obviously, the integral appearing in the previous expression diverges at both large and small
is small,
Obviously, the integral appearing in the previous expression diverges at both large and small 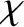 .
.
The divergence of the integral on the right-hand side of the previous equation at large 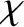 is a consequence of the breakdown of the small-angle approximation. The standard prescription
for avoiding this divergence is to truncate the integral at some
is a consequence of the breakdown of the small-angle approximation. The standard prescription
for avoiding this divergence is to truncate the integral at some
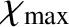 above which the small-angle approximation becomes
invalid. According to Equation (3.84), this truncation is equivalent to neglecting all collisions whose impact parameters
fall below the value
above which the small-angle approximation becomes
invalid. According to Equation (3.84), this truncation is equivalent to neglecting all collisions whose impact parameters
fall below the value
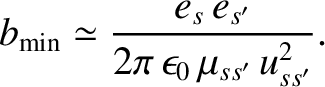 |
(3.115) |
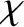 is the idea that Coulomb collisions are dominated by small-angle scattering events, and that
the occasional large-angle scattering events have a negligible effect on the scattering statistics. Unfortunately, this is not quite true (if it were then the integral would converge at large
is the idea that Coulomb collisions are dominated by small-angle scattering events, and that
the occasional large-angle scattering events have a negligible effect on the scattering statistics. Unfortunately, this is not quite true (if it were then the integral would converge at large 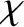 ). However, the
rare large-angle scattering events only make a relatively weak logarithmic contribution to the scattering statistics.
). However, the
rare large-angle scattering events only make a relatively weak logarithmic contribution to the scattering statistics.
Making the estimate
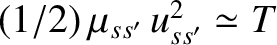 , where
, where 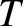 is the assumed common temperature of the
two colliding species, we obtain
is the assumed common temperature of the
two colliding species, we obtain
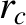 is the classical distance of closest approach introduced in Section 1.6.
However, as mentioned in Section 1.10, it is possible for the classical distance of closest approach
to fall below the de Broglie wavelength of one or both of the colliding particles, even in the case of a weakly coupled plasma.
In this situation, the most sensible thing to do is to approximate
is the classical distance of closest approach introduced in Section 1.6.
However, as mentioned in Section 1.10, it is possible for the classical distance of closest approach
to fall below the de Broglie wavelength of one or both of the colliding particles, even in the case of a weakly coupled plasma.
In this situation, the most sensible thing to do is to approximate
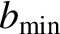 as the larger de Broglie wavelength (Spitzer 1956; Braginskii 1965).
as the larger de Broglie wavelength (Spitzer 1956; Braginskii 1965).
The divergence of the integral on the right-hand side of Equation (3.114) at small 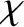 is a consequence of the
infinite range of the Coulomb potential. The standard prescription
for avoiding this divergence is to take the Debye shielding of the Coulomb potential into account. (See Section 1.5.) This is equivalent to
neglecting all collisions whose impact parameters exceed the value
is a consequence of the
infinite range of the Coulomb potential. The standard prescription
for avoiding this divergence is to take the Debye shielding of the Coulomb potential into account. (See Section 1.5.) This is equivalent to
neglecting all collisions whose impact parameters exceed the value
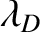 is the Debye length. Of course, Debye shielding is a many-particle effect. Hence, the Landau collision operator can no longer be regarded as a
pure two-body collision operator. Fortunately, however, many-particle effects only make a relatively weak logarithmic contribution to the operator.
is the Debye length. Of course, Debye shielding is a many-particle effect. Hence, the Landau collision operator can no longer be regarded as a
pure two-body collision operator. Fortunately, however, many-particle effects only make a relatively weak logarithmic contribution to the operator.
According to Equations (3.86), (3.116), and (3.117),
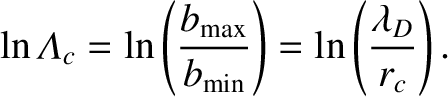 |
(3.118) |
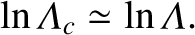 |
(3.119) |
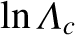 lies in the range
lies in the range
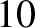 –
–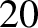 for typical weakly coupled plasmas. It also follows that
for typical weakly coupled plasmas. It also follows that
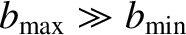 in a
weakly coupled plasma, which means that there is a large range of impact parameters for which it is accurate to treat Coulomb collisions
as small-angle two-body scattering events.
in a
weakly coupled plasma, which means that there is a large range of impact parameters for which it is accurate to treat Coulomb collisions
as small-angle two-body scattering events.
The conventional definition of the Coulomb logarithm is as follows (Richardson 2019). For a species- particle,
with mass
particle,
with mass 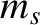 , charge
, charge 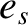 , number density
, number density 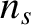 , and temperature
, and temperature 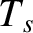 , scattered by species-
, scattered by species-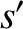 particles, with mass
particles, with mass 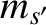 , charge
, charge 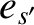 ,
number density
,
number density 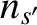 , and temperature
, and temperature 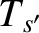 ,
the Coulomb logarithm is defined
,
the Coulomb logarithm is defined
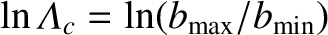 . Here,
. Here,
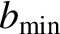 is the larger of
is the larger of
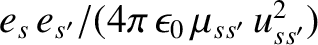 and
and
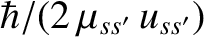 , averaged over both particle
distributions, where
, averaged over both particle
distributions, where
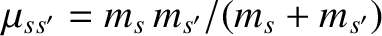 and
and
 . Furthermore,
. Furthermore,
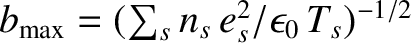 , where the
summation extends over all species,
, where the
summation extends over all species,  , for which
, for which
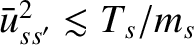 .
.
Consider a quasi-neutral plasma consisting of electrons of mass 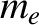 , charge
, charge 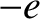 , number density
, number density 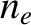 ,
and temperature
,
and temperature 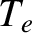 , and ions of mass
, and ions of mass 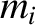 , charge
, charge 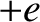 , number density
, number density 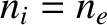 , and temperature
, and temperature 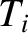 .
For thermal (i.e., Maxwellian) electron-electron collisions, we obtain (Richardson 2019)
.
For thermal (i.e., Maxwellian) electron-electron collisions, we obtain (Richardson 2019)
![$\displaystyle \ln{\mit\Lambda}_c = 23.5 - \ln\left(n_e^{1/2}\,T_e^{-5/4}\right)-\left[10^{-5} + (\ln T_e-2)^2/16\right]^{1/2}.$](img840.png) |
(3.120) |
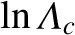 |
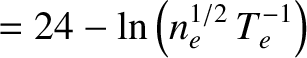 |
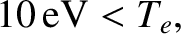 |
||
 |
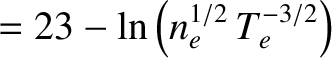 |
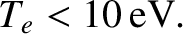 |
(3.121) |
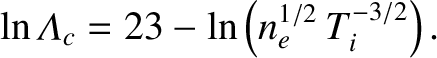 |
(3.122) |
 is measured in units of
is measured in units of
 , and all species temperatures are measured in units of
electron-volts.
, and all species temperatures are measured in units of
electron-volts.
The standard approach in plasma physics is to treat the Coulomb logarithm as a constant, with a value determined by the ambient
electron number density, and the ambient electron and ion temperatures, as has just been described. This approximation ensures that the Landau collision
operator,
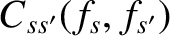 , is strictly bilinear in its two arguments.
, is strictly bilinear in its two arguments.