


Next: Ponomarenko Dynamo
Up: Magnetohydrodynamic Fluids
Previous: Slow and Fast Dynamos
One of the most important results in slow, kinematic dynamo theory
is credited to Cowling (Cowling 1934; Cowling 1957b). The so-called Cowling anti-dynamo theorem
states that:
An axisymmetric magnetic field cannot be maintained via dynamo action.
Let us attempt to prove this proposition.
We adopt standard cylindrical coordinates:
 . The
system is assumed to possess axial symmetry, so that
. The
system is assumed to possess axial symmetry, so that
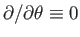 . For the sake of simplicity, the plasma flow is assumed to be
incompressible, which implies that
. For the sake of simplicity, the plasma flow is assumed to be
incompressible, which implies that
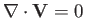 .
.
It is convenient to split the magnetic and velocity fields into poloidal
and toroidal components:
Here, a ``poloidal'' vector only possesses non-zero 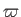 - and
- and 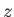 -components,
whereas a ``toroidal'' vector only possesses a non-zero
-components,
whereas a ``toroidal'' vector only possesses a non-zero 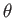 -component.
-component.
The poloidal components of the magnetic and velocity fields are
written (Huba 2000a),
where
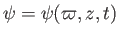 and
and
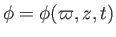 . The
toroidal components are given by
. The
toroidal components are given by
Note that by writing the 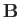 and
and  fields in the previous form
we ensure that the constraints
fields in the previous form
we ensure that the constraints
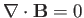 and
and
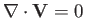 are automatically satisfied. Note, further,
that because
are automatically satisfied. Note, further,
that because
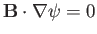 and
and
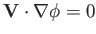 ,
we can regard
,
we can regard 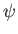 and
and 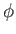 as stream-functions for the magnetic and
velocity fields, respectively.
as stream-functions for the magnetic and
velocity fields, respectively.
The condition for the magnetic field to be maintained by dynamo currents,
rather than by currents at infinity, is
where
 . We also require the flow stream-function,
. We also require the flow stream-function,
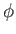 , to remain bounded as
, to remain bounded as
 .
.
Consider the MHD Ohm's law for a resistive plasma:
 |
(7.122) |
Taking the toroidal component of this equation, we obtain
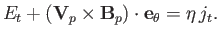 |
(7.123) |
It is easily demonstrated from the Faraday-Maxwell equation that
 |
(7.124) |
Furthermore,
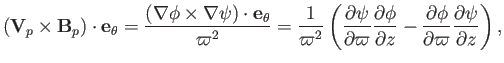 |
(7.125) |
and (Huba 2000a)
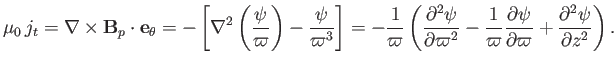 |
(7.126) |
Thus,
Equation (7.123) reduces to
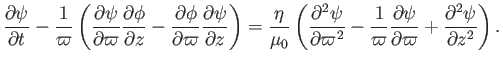 |
(7.127) |
Multiplying the previous equation by 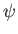 and integrating over all space,
we obtain
and integrating over all space,
we obtain
The second term on the left-hand side of the previous expression
can be integrated by parts to give
![$\displaystyle -\int\!\!\int 2\pi\left[-\phi\,\frac{\partial}{\partial z} \left(...
...varpi}\left(\psi\,\frac{\partial\psi}{\partial z} \right)\right] d\varpi\,dz=0,$](img2540.png) |
(7.129) |
where surface terms have been neglected, in accordance with Equation (7.121).
Likewise, the term on the right-hand side of Equation (7.128) can be integrated by
parts to give
![$\displaystyle \frac{\eta}{\mu_0}\int\!\!\int 2\pi\left[-\frac{\partial(\varpi\,...
...} - \varpi\left(\frac{\partial\psi} {\partial z}\right)^2\right]\,d\varpi\,d z=$](img2541.png) |
|
![$\displaystyle -\frac{\eta}{\mu_0}\int\!\!\int 2\pi\, \varpi\left[\left(\frac{\p...
...}\right)^2 +\left(\frac{\partial\psi}{\partial z}\right)^2\right]\,d\varpi\,dz.$](img2542.png) |
|
(7.130) |
Thus, Equation (7.128) reduces to
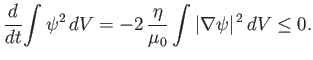 |
(7.131) |
It is clear, from the previous expression, that the poloidal stream-function, 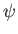 --and, hence, the poloidal magnetic field,
--and, hence, the poloidal magnetic field, 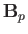 --decays to zero
under the influence of resistivity. We conclude that the poloidal magnetic
field cannot be maintained via dynamo action.
--decays to zero
under the influence of resistivity. We conclude that the poloidal magnetic
field cannot be maintained via dynamo action.
Of course, we have not ruled out the possibility that the toroidal magnetic
field can be maintained via dynamo action. In the absence of a poloidal
field, the curl of the poloidal component of Equation (7.122) yields
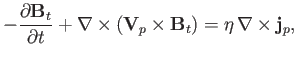 |
(7.132) |
which reduces to
 |
(7.133) |
Now (Huba 2000a),
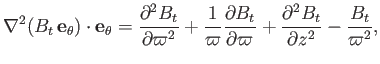 |
(7.134) |
and (Huba 2000a)
 |
(7.135) |
Thus, Equation (7.133) yields
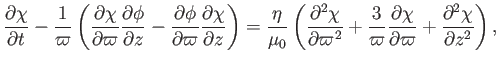 |
(7.136) |
where
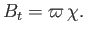 |
(7.137) |
Multiply Equation (7.136) by 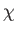 , integrating over all space, and
then integrating by parts, we obtain
, integrating over all space, and
then integrating by parts, we obtain
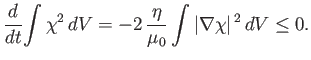 |
(7.138) |
It is clear, from this equation, that 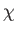 --and, hence, the toroidal magnetic
field,
--and, hence, the toroidal magnetic
field,  --decays to zero under the influence of resistivity.
We conclude that no axisymmetric magnetic field--either poloidal
or toroidal--can be maintained by
dynamo action, which proves Cowling's theorem.
--decays to zero under the influence of resistivity.
We conclude that no axisymmetric magnetic field--either poloidal
or toroidal--can be maintained by
dynamo action, which proves Cowling's theorem.
Cowling's theorem is the earliest, and most significant, of a number of
anti-dynamo theorems that severely restrict the types of magnetic
fields that can be maintained via dynamo action. For instance, it is
possible to prove that a two-dimensional magnetic field cannot be maintained
by dynamo action (Moffatt 1978). Here, ``two-dimensional'' implies that in some
Cartesian coordinate system,
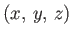 , the magnetic field is independent of
, the magnetic field is independent of
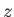 . The suite of anti-dynamo theorems can be summed up
by saying that successful dynamos possess a rather low degree of symmetry.
. The suite of anti-dynamo theorems can be summed up
by saying that successful dynamos possess a rather low degree of symmetry.



Next: Ponomarenko Dynamo
Up: Magnetohydrodynamic Fluids
Previous: Slow and Fast Dynamos
Richard Fitzpatrick
2016-01-23
![]() . The
system is assumed to possess axial symmetry, so that
. The
system is assumed to possess axial symmetry, so that
![]() . For the sake of simplicity, the plasma flow is assumed to be
incompressible, which implies that
. For the sake of simplicity, the plasma flow is assumed to be
incompressible, which implies that
![]() .
.
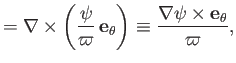
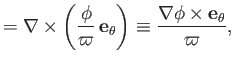

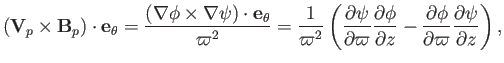
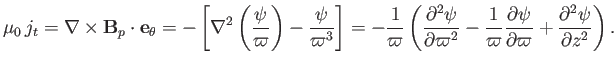
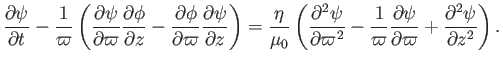
![]() and integrating over all space,
we obtain
and integrating over all space,
we obtain
![$\displaystyle -\int\!\!\int 2\pi\left[-\phi\,\frac{\partial}{\partial z} \left(...
...varpi}\left(\psi\,\frac{\partial\psi}{\partial z} \right)\right] d\varpi\,dz=0,$](img2540.png)
![$\displaystyle \frac{\eta}{\mu_0}\int\!\!\int 2\pi\left[-\frac{\partial(\varpi\,...
...} - \varpi\left(\frac{\partial\psi} {\partial z}\right)^2\right]\,d\varpi\,d z=$](img2541.png)
![$\displaystyle -\frac{\eta}{\mu_0}\int\!\!\int 2\pi\, \varpi\left[\left(\frac{\p...
...}\right)^2 +\left(\frac{\partial\psi}{\partial z}\right)^2\right]\,d\varpi\,dz.$](img2542.png)
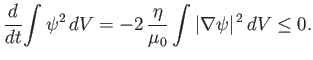
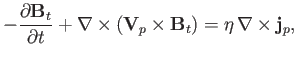
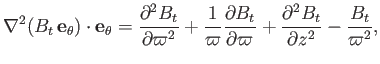

![]() , integrating over all space, and
then integrating by parts, we obtain
, integrating over all space, and
then integrating by parts, we obtain
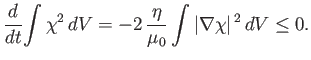
![]() , the magnetic field is independent of
, the magnetic field is independent of
![]() . The suite of anti-dynamo theorems can be summed up
by saying that successful dynamos possess a rather low degree of symmetry.
. The suite of anti-dynamo theorems can be summed up
by saying that successful dynamos possess a rather low degree of symmetry.