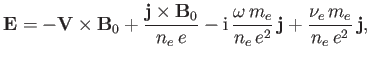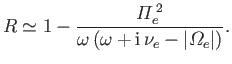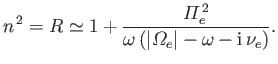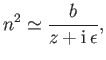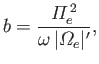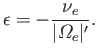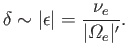Next: Pulse Propagation
Up: Wave Propagation Through Inhomogeneous
Previous: Resonant Layers
Collisional Damping
Let us now consider a real-life damping mechanism. Equation (5.15)
specifies the linearized Ohm's law in the collisionless
cold-plasma approximation.
In the presence of collisions, this expression acquires
an extra term (see Section 4.12), such that
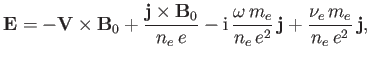 |
(6.62) |
where
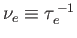 is the electron collision frequency. Here, for the sake of simplicity,
we have neglected the small difference between the parallel and perpendicular
plasma electrical conductivities. When
Equation (6.62) is used to calculate the dielectric permittivity for a
right-handed wave, in the limit
is the electron collision frequency. Here, for the sake of simplicity,
we have neglected the small difference between the parallel and perpendicular
plasma electrical conductivities. When
Equation (6.62) is used to calculate the dielectric permittivity for a
right-handed wave, in the limit
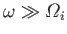 , we obtain
, we obtain
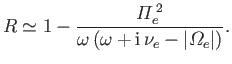 |
(6.63) |
A right-handed circularly polarized wave, propagating parallel to the
magnetic field, is governed by the dispersion relation (see Section 5.9)
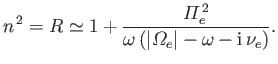 |
(6.64) |
Suppose that 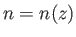 . Furthermore, let
. Furthermore, let
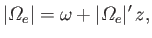 |
(6.65) |
so that the electron cyclotron resonance is located at  .
We also assume that
.
We also assume that
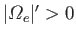 , so that the evanescent region
corresponds to
, so that the evanescent region
corresponds to 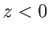 .
It follows that, in the immediate vicinity of the resonance,
.
It follows that, in the immediate vicinity of the resonance,
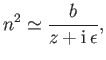 |
(6.66) |
where
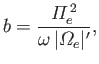 |
(6.67) |
and
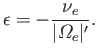 |
(6.68) |
It can be seen that
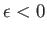 , which is consistent with the
absorption of incident wave energy by the resonant layer. The
approximate width of the resonant layer
is
, which is consistent with the
absorption of incident wave energy by the resonant layer. The
approximate width of the resonant layer
is
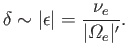 |
(6.69) |
Note that the damping mechanism--in this case collisions--controls the
thickness of the resonant layer, but does not control the
amount of wave energy absorbed by the layer. In fact, in the simple
theory outlined previously,
all of the incident wave energy is absorbed by the layer.



Next: Pulse Propagation
Up: Wave Propagation Through Inhomogeneous
Previous: Resonant Layers
Richard Fitzpatrick
2016-01-23