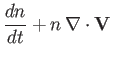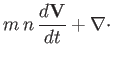Next: Braginskii Equations
Up: Plasma Fluid Theory
Previous: Chapman-Enskog Closure
Normalization of Neutral Gas Equations
Let 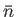 ,
, 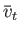 , and
, and 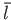 be typical values of the
particle density, the thermal velocity, and the mean-free-path, respectively.
Suppose that the typical flow velocity is
be typical values of the
particle density, the thermal velocity, and the mean-free-path, respectively.
Suppose that the typical flow velocity is
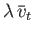 ,
and the typical variation lengthscale of macroscopic quantities is
,
and the typical variation lengthscale of macroscopic quantities is 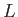 . Let us
define the following normalized quantities:
. Let us
define the following normalized quantities:
Here,
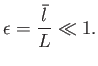 |
(4.70) |
Note that
All hatted quantities are designed to be
 .
The normalized fluid equations are written:
.
The normalized fluid equations are written:
where
 |
(4.76) |
The only large or small quantities remaining in the previous equations are
the parameters  and
and  .
.
Suppose that
 . In other words, suppose that the flow velocity is much
greater than the thermal speed. Retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
. In other words, suppose that the flow velocity is much
greater than the thermal speed. Retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
These are called the cold-gas equations, because they can also
be obtained by formally taking the limit
 . The cold-gas
equations describe
externally driven, highly supersonic, gas dynamics.
The gas pressure (that is, the thermal energy density)
can be neglected in the cold-gas limit, because the thermal velocity is much
smaller than the flow velocity. Consequently, there is no need for an energy evolution equation. Furthermore, the
viscosity can also be neglected, because the
viscous diffusion velocity is also far smaller than the
flow velocity.
. The cold-gas
equations describe
externally driven, highly supersonic, gas dynamics.
The gas pressure (that is, the thermal energy density)
can be neglected in the cold-gas limit, because the thermal velocity is much
smaller than the flow velocity. Consequently, there is no need for an energy evolution equation. Furthermore, the
viscosity can also be neglected, because the
viscous diffusion velocity is also far smaller than the
flow velocity.
Suppose that
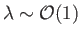 . In other words, suppose the flow velocity is of similar magnitude to the
thermal speed. Again, retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
. In other words, suppose the flow velocity is of similar magnitude to the
thermal speed. Again, retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
The previous equations can be rearranged to give:
These are called the hydrodynamic equations, because they are similar to the
equations governing the dynamics of water. The hydrodynamic equations
govern relatively fast, internally driven,
gas dynamics--in particular, the dynamics of sound waves.
The gas pressure is non-negligible in the
hydrodynamic limit, because the
thermal velocity is similar in magnitude to the flow speed.
Consequently, an energy evolution equation is needed. However, the
energy equation takes a particularly simple form, as
Equation (4.84) is immediately recognizable as the adiabatic equation
of state for a monatomic gas. This is not surprising, because the
flow velocity is still much faster than the viscous and thermal diffusion
velocities (which accounts for the absence of viscosity and thermal conductivity in the
hydrodynamic equations), in which case the gas acts effectively like a perfect
thermal insulator.
Suppose, finally, that
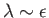 . In other words, suppose the flow
velocity is of similar magnitude to the viscous and thermal diffusion velocities. Our system
of fluid equations now reduces to a force balance criterion,
. In other words, suppose the flow
velocity is of similar magnitude to the viscous and thermal diffusion velocities. Our system
of fluid equations now reduces to a force balance criterion,
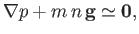 |
(4.85) |
to lowest order. To next order, we obtain a set of equations
describing the relatively slow viscous and thermal evolution
of the gas:
Clearly, this set of equations is only appropriate to relatively quiescent,
quasi-equilibrium, gas dynamics. Virtually all of the terms
in our original fluid equations, (4.55)-(4.57), must be retained in this limit.
The previous investigation reveals an important truth in gas dynamics, which also
applies to plasma dynamics. Namely, the form of the
fluid equations crucially depends on the typical fluid velocity
associated with the type of dynamics under investigation. As a general rule,
the equations get simpler as the typical velocity gets faster, and vice versa.



Next: Braginskii Equations
Up: Plasma Fluid Theory
Previous: Chapman-Enskog Closure
Richard Fitzpatrick
2016-01-23
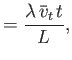
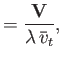
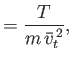
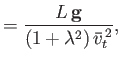
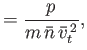
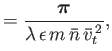
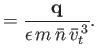
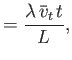
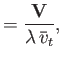
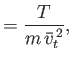
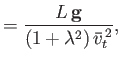
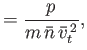
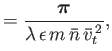
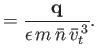
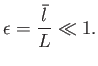
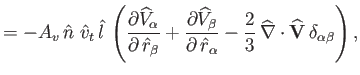
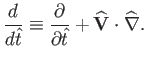
![]() . In other words, suppose that the flow velocity is much
greater than the thermal speed. Retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
. In other words, suppose that the flow velocity is much
greater than the thermal speed. Retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
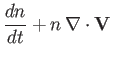
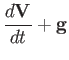
![]() . In other words, suppose the flow velocity is of similar magnitude to the
thermal speed. Again, retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
. In other words, suppose the flow velocity is of similar magnitude to the
thermal speed. Again, retaining only the largest terms in Equations (4.73)-(4.75),
our system of fluid equations reduces to (in unnormalized form):
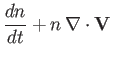
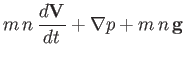
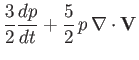
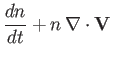
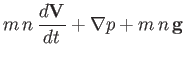
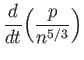
![]() . In other words, suppose the flow
velocity is of similar magnitude to the viscous and thermal diffusion velocities. Our system
of fluid equations now reduces to a force balance criterion,
. In other words, suppose the flow
velocity is of similar magnitude to the viscous and thermal diffusion velocities. Our system
of fluid equations now reduces to a force balance criterion,