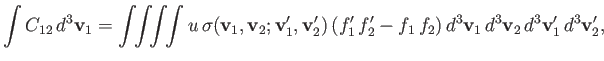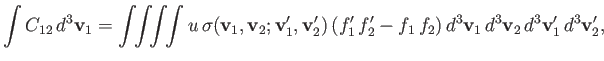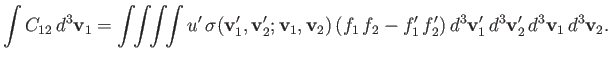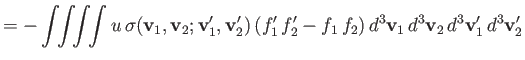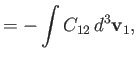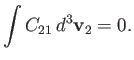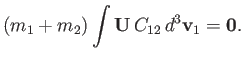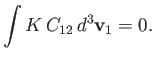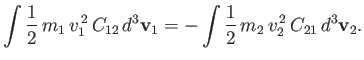Next: Boltzmann H-Theorem
Up: Collisions
Previous: Boltzmann Collision Operator
Collisional Conservation Laws
Consider
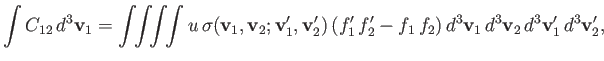 |
(3.25) |
which follows from Equation (3.20).
Interchanging primed and unprimed dummy variables of integration on the right-hand side, we
obtain
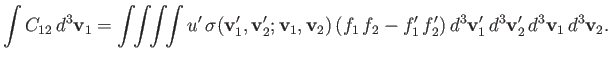 |
(3.26) |
Hence, making use of Equation (3.16), as well as the fact that  , we
deduce that
, we
deduce that
which implies that
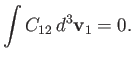 |
(3.28) |
The previous expression states that collisions with particles of type  give rise to zero net rate of change of the number density of particles of type
give rise to zero net rate of change of the number density of particles of type  at position
at position  and time
and time 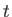 . In other words, the collisions conserve the number of particles of type
. In other words, the collisions conserve the number of particles of type  .
Now, it is easily seen from Equations (3.20) and (3.21) that
.
Now, it is easily seen from Equations (3.20) and (3.21) that
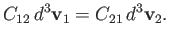 |
(3.29) |
Hence, Equation (3.28) also implies that
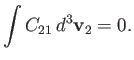 |
(3.30) |
In other words, collisions also conserve the number of particles of type  .
.
Consider
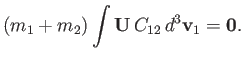 |
(3.31) |
This integral is obviously zero, as indicated, as a consequence of the conservation law (3.28), as well as the fact that the center
of mass velocity,  , is a constant of the motion. However, making use of Equations (3.10) and (3.29), the
previous expression can be rewritten in the form
, is a constant of the motion. However, making use of Equations (3.10) and (3.29), the
previous expression can be rewritten in the form
 |
(3.32) |
This equation states that the rate at which particles of type  gain momentum due to collisions with particles of type
gain momentum due to collisions with particles of type  is equal
to the rate at which particles of type
is equal
to the rate at which particles of type  lose momentum due to collisions with particles of type
lose momentum due to collisions with particles of type  . In other words, the collisions
conserve momentum.
. In other words, the collisions
conserve momentum.
Finally, consider
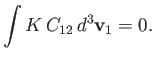 |
(3.33) |
This integral is obviously zero, as indicated, as a consequence of the conservation law (3.28), as well as the fact that the kinetic
energy, 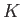 , is the same before and after an elastic collision. It follows from Equations (3.15) and (3.29) that
, is the same before and after an elastic collision. It follows from Equations (3.15) and (3.29) that
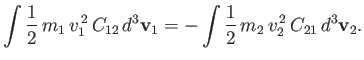 |
(3.34) |
This equation states that the rate at which particles of type  gain kinetic energy due to collisions with particles of type
gain kinetic energy due to collisions with particles of type  is equal
to the rate at which particles of type
is equal
to the rate at which particles of type  lose kinetic energy due to collisions with particles of type
lose kinetic energy due to collisions with particles of type  .
In other words, the collisions conserve energy.
.
In other words, the collisions conserve energy.



Next: Boltzmann H-Theorem
Up: Collisions
Previous: Boltzmann Collision Operator
Richard Fitzpatrick
2016-01-23