Next: Boltzmann Collision Operator
Up: Collisions
Previous: Collision Operator
Two-Body Elastic Collisions
Before specializing to two-body Coulomb collisions, it is convenient to develop a general theory of two-body elastic collisions.
Consider an elastic collision between a particle of type  and a particle of type
and a particle of type  . Let the mass and instantaneous velocity of the former particle be
. Let the mass and instantaneous velocity of the former particle be 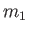 and
and 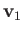 , respectively. Likewise, let the
mass and
instantaneous velocity of the latter particle be
, respectively. Likewise, let the
mass and
instantaneous velocity of the latter particle be 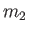 and
and 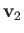 , respectively. The velocity of the
center of mass is given by
, respectively. The velocity of the
center of mass is given by
 |
(3.10) |
Moreover, conservation of momentum implies that  is a constant of the motion. The relative velocity is
defined
is a constant of the motion. The relative velocity is
defined
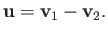 |
(3.11) |
We can express 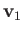 and
and 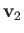 in terms of
in terms of  and
and  as follows:
as follows:
Here,
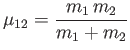 |
(3.14) |
is the reduced mass.
The total kinetic energy of the system is written
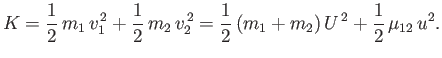 |
(3.15) |
Now, the kinetic energy is the same before and after an elastic collision. Hence, given that  is constant, we deduce that the
magnitude of the relative velocity,
is constant, we deduce that the
magnitude of the relative velocity, 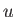 , is also the same before and after such a collision. Thus, it is only the direction of the
relative velocity vector, rather than its length, that changes during an elastic collision.
, is also the same before and after such a collision. Thus, it is only the direction of the
relative velocity vector, rather than its length, that changes during an elastic collision.



Next: Boltzmann Collision Operator
Up: Collisions
Previous: Collision Operator
Richard Fitzpatrick
2016-01-23