Next: Magnetic Mirrors
Up: Charged Particle Motion
Previous: Poincaré Invariants
Adiabatic Invariants
Poincaré invariants are generally of little practical interest
unless the curve  closely corresponds to the trajectories of
actual particles. For the motion of magnetized particles,
it is evident from Equations (2.25), (2.38), and (2.40) that points having the same
guiding center at a certain time will continue to have approximately
the same guiding center at later times. An approximate Poincaré
invariant may thus be obtained by choosing the curve
closely corresponds to the trajectories of
actual particles. For the motion of magnetized particles,
it is evident from Equations (2.25), (2.38), and (2.40) that points having the same
guiding center at a certain time will continue to have approximately
the same guiding center at later times. An approximate Poincaré
invariant may thus be obtained by choosing the curve 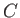 to be a circle of points
corresponding to a gyrophase period. In other words,
to be a circle of points
corresponding to a gyrophase period. In other words,
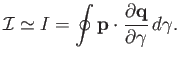 |
(2.75) |
Here, 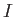 is an adiabatic invariant.
is an adiabatic invariant.
To evaluate 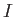 for a magnetized plasma recall that the canonical momentum
for charged particles is (Jackson 1998)
for a magnetized plasma recall that the canonical momentum
for charged particles is (Jackson 1998)
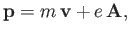 |
(2.76) |
where 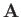 is the vector potential. Let us express
is the vector potential. Let us express 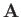 in terms
of its Taylor series about the guiding center position:
in terms
of its Taylor series about the guiding center position:
The element of length along the curve 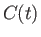 is [see Equation (2.39)]
is [see Equation (2.39)]
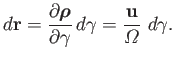 |
(2.78) |
The adiabatic invariant is thus
![$\displaystyle I = \oint \frac{{\bf u}}{{\mit\Omega}} \cdot \left( m\,[{\bf U} +...
...oldmath$\rho$}\cdot \nabla)\,{\bf A}\right]\right)d\gamma + {\cal O}(\epsilon),$](img382.png) |
(2.79) |
which reduces to
The final term on the right-hand side is written [see Equations (2.41) and (2.44)]
It follows that
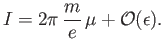 |
(2.82) |
Thus, to lowest order, the adiabatic invariant is proportional to the magnetic moment, 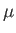 .
.



Next: Magnetic Mirrors
Up: Charged Particle Motion
Previous: Poincaré Invariants
Richard Fitzpatrick
2016-01-23
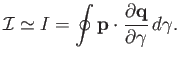
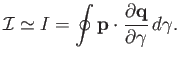
![]() for a magnetized plasma recall that the canonical momentum
for charged particles is (Jackson 1998)
for a magnetized plasma recall that the canonical momentum
for charged particles is (Jackson 1998)
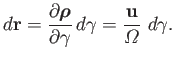
![$\displaystyle I = \oint \frac{{\bf u}}{{\mit\Omega}} \cdot \left( m\,[{\bf U} +...
...oldmath$\rho$}\cdot \nabla)\,{\bf A}\right]\right)d\gamma + {\cal O}(\epsilon),$](img382.png)